Accelerated and Sparse Algorithms for Approximate Personalized PageRank and Beyond
TL;DR: This is an informal discussion of our recent paper Accelerated and Sparse Algorithms for Approximate Personalized PageRank and Beyond by David Martinez-Rubio, Elias Wirth, and Sebastian Pokutta. We answer the open question to the COLT 2022 open problem by Fountoulakis and Yang [FY] in the affirmative, presenting sparse accelerated optimization algorithms for the $\ell_1$-regularized personalized PageRank problem.
Written by Elias Wirth.
Introduction
With the rise of large-scale networks, the study of local graph clustering has gained significant attention, fueling extensive research into local graph clustering algorithms [FY, FRS]. When graphs become large in the number of vertices and edges, practitioners run into memory issues. Thus, local algorithms operate only on a local subset of vertices and edges of the graph. At the heart of local graph clustering is the approximate personalized PageRank algorithm (APPR) [ACL], which offers an approximation to the solution of the PageRank linear system [PBM] within an undirected graph. This technique rounds the approximate solution to reveal local partitions within the graph’s structure.
Although the output of APPR doesn’t inherently present itself as the solution to an optimization problem, recent advancements by Fountoulakis et al. [FRS] introduced a variational formulation of local graph clustering as an $\ell_1$-regularized convex optimization problem, which Fountoulakis et al. solved using the iterative shrinkage-thresholding algorithm (ISTA) [PB]. Subsequently, Fountoulakis and Yang [FY] then raised the question whether the variational formulation could be addressed with accelerated methods whose per iteration complexity does not depend on the size of the whole graph, but on the size of local objects like the support of solution or its set of neighbors, the fast iterative shrinkage-threshholding algorithm (FISTA) [PB]. We answer this question in the affirmative by presenting several accelerated methods.
Preliminaries
We briefly recall the problem formulation. We are given an undirected graph $G = (V, E)$, where $V$ and $E$ are the vertex and edge set, respectively. Let $n$ denote the number of vertices. Let $A$, $D$, and $L = I - D^{-1/2}A D^{-1/2}$ denote the associated adjacency, degree, and Laplacian matrices, respectively. Given a parameter $\alpha \in ]0, 1[$, we further define the positive definite matrix
\[\begin{align*} Q = \alpha I + \frac{1-\alpha}{2}L, \end{align*}\]which satisfies $\alpha I \preccurlyeq Q \preccurlyeq 2 I$. Then, the variational formulation derived in [FRS] boils down to solving the constrained convex optimization problem
\[\begin{align*} \tag{OPT} \min_{x\in\mathbb{R}_{\geq 0}} g(x), \end{align*}\]where
\[\begin{align*} g(x) = \frac{1}{2} \langle x, Qx\rangle + \alpha \langle -D^{-1/2}s + \rho D^{1/2}\mathbf{1}, x\rangle \end{align*}\]and $s\in\Delta_n$ is a probability distribution over the vertices of $G$ called teleportation distribution and $\rho\in [0, 1]$ is the regularization parameter.
Let
\[\begin{align*} x^\esx := \text{argmin}_{x\in\mathbb{R}_{\geq 0}} g(x) \end{align*}\]denote the optimal solution with support \(S^\esx := \text{supp}(x^\esx)\). Note that for our setting, we generally have \(\lvert S^\esx \rvert << n\), that is, the optimizer is highly sparse.
Finally, for a subset of vertices $S \subseteq V$, we define the volume of $S$ as \(\text{vol}(S) := \sum_{i \in S} d_i + \lvert S \rvert\), that is, as the sum of the degrees of vertices in $S$, plus \(\lvert S \rvert\) and the internal volume of $S$ as $\tilde{\text{vol}}(S) := \lvert S \rvert + \sum_{(i,j) \in E} \mathbf{1}_{\lbrace i,j \in S\rbrace}$, that is, as the sum of edges of the subgraph induced by $S$, plus $\lvert S \rvert$.
Contributions
We extend the geometrical observations from [FRS] to derive four new algorithms for (OPT), all of which are accelerated in the sense that their time complexities are either completely independent of the condition number \(\frac{1}{\alpha}\) or improve the dependence to \(\frac{1}{\sqrt{\alpha}}\) compared to ISTA’s time complexity of order \(\tilde{O}(\text{vol}(S^\esx \frac{1}{\alpha})\). We thus answer the open question in [FY] in the affirmative, providing multiple accelerated algorithms for (OPT). Note that all our algorithms are local, that is, generally don’t access the full graph and consequently, the per-iteration cost is not in \(O(n)\) but depends on \(O(\abs{N(S^\esx)})\) instead, where \(N(S^\esx)\) denotes the neighbourhood of \(S^\esx\).
| Algorithm | Time complexity | Space complexity |
|---|---|---|
| ISTA [FRS] | \(\tilde{O}(\text{vol}(S^\esx) \frac{1}{\alpha})\) | \(O(\lvert S^\esx \rvert )\) |
| Conjugate directions PageRank algorithm (CDPR) | \(O(\lvert S^\esx \rvert^3 + \lvert S^\esx \rvert \text{vol}(S^\esx))\) | \(O(\lvert S^\esx \rvert^2 )\) |
| Accelerated sparse PageRank (ASPR) | \(\tilde{O}(\lvert S^\esx \rvert \tilde{\text{vol}}( S^\esx ) \frac{1}{\sqrt{\alpha}} + \lvert S^\esx \rvert \text{vol}(S^\esx))\) | \(O(\lvert S^\esx \rvert )\) |
| Conjugate-gradients ASPR (CASPR) | \(\tilde{O}(\lvert S^\esx \rvert \tilde{\text{vol}}( S^\esx ) \min\lbrace \frac{1}{\sqrt{\alpha}}, \lvert S^\esx \rvert \rbrace + \lvert S^\esx \rvert \text{vol}(S^\esx))\) | \(O(\lvert S^\esx \rvert )\) |
| Laplacian-solver ASPR (LASPR) | \(\tilde{O}(\lvert S^\esx \rvert \tilde{\text{vol}}( S^\esx )) + O( \lvert S^\esx \rvert \text{vol}( S^\esx ))\) | \(O(\lvert S^\esx \rvert )\) |
Our contribution extends beyond theory, as we offer complete julia implementations of all algorithms (excluding LASPR due to numerical instability) on GitHub. In our numerical experiments, we find that CASPR remarkably outperforms other algorithms in terms of solution sparsity and runtime efficiency. We compare the performance of all algorithms on the patent_cit_us [LK] graph consisting of 3,774,768 vertices and 16,518,948 edges. In the paper, we compare the methods on several other graphs, but the results are similar across problem instances. The parameters are $\alpha=0.01$ and $\rho=0.0001$ and the algorithms are run up to accuracy $\epsilon=10^{-6}$.
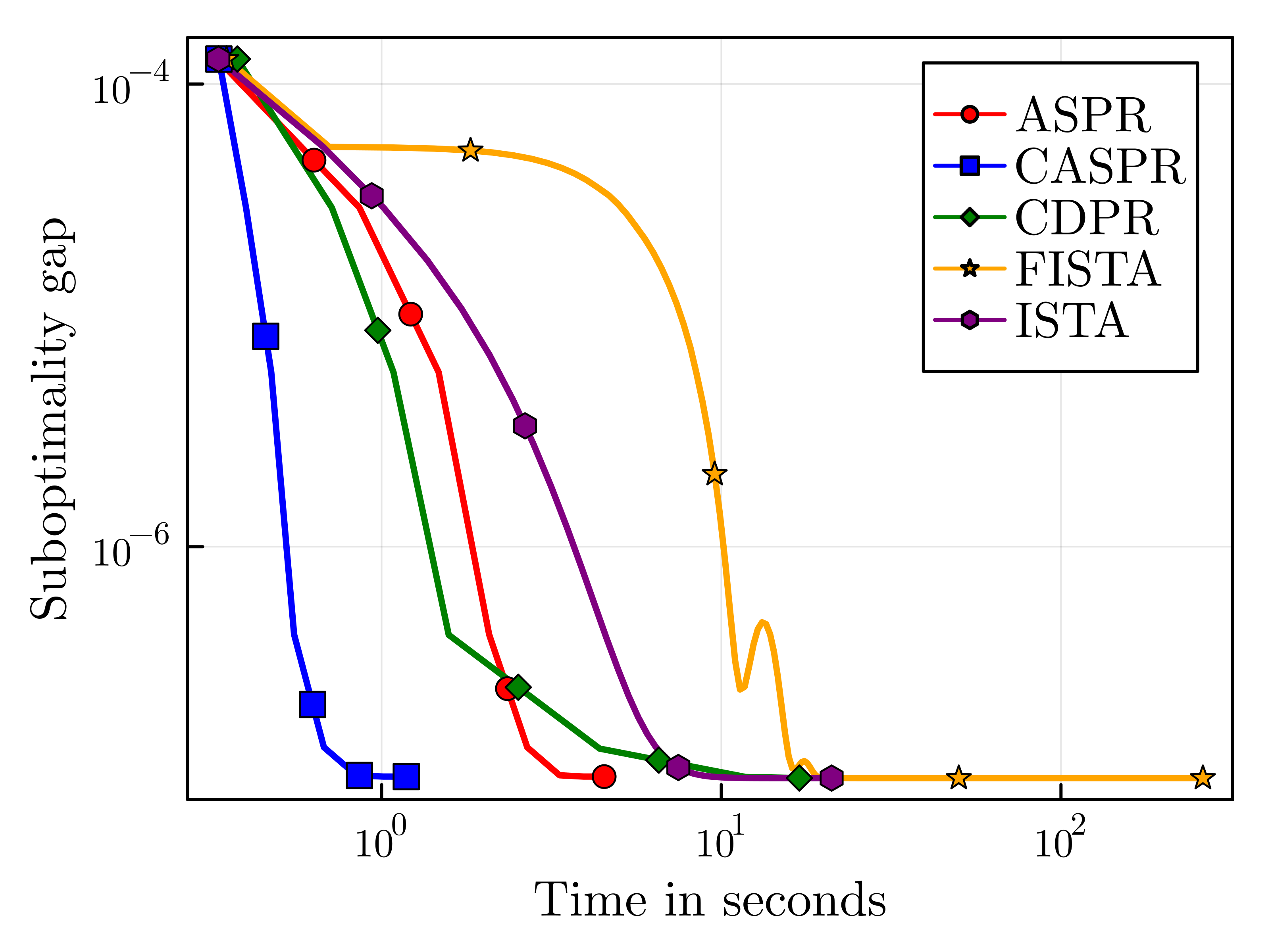

Figure 1. Running time comparison (left) and sparsity comparison (right)
References
[ACL] Reid Andersen, Fan R. K. Chung, and Kevin J. Lang. “Local Graph Partitioning using PageRank Vectors”. In: 47th Annual IEEE Symposium on Foundations of Computer Science (FOCS 2006), 21-24 October 2006, Berkeley, California, USA, Proceedings. IEEE Computer Society, 2006, pp. 475–486.
[FRS] Kimon Fountoulakis, Farbod Roosta-Khorasani, Julian Shun, Xiang Cheng, and Michael W Mahoney. “Variational perspective on local graph clustering”. In: Mathematical Programming 174.1 (2019), pp. 553–573.
[FY] Kimon Fountoulakis and Shenghao Yang. “Open Problem: Running time complexity of accelerated ℓ1-regularized PageRank”. In: Proceedings of the Conference on Learning Theory. PMLR. 2022, pp. 5630–5632.
[LK] Jure Leskovec and Andrej Krevl. SNAP Datasets: Stanford Large Network Dataset Collection. http:// snap.stanford.edu/ data. June 2014.
[PB] Neal Parikh and Stephen P. Boyd. “Proximal Algorithms”. In: Found. Trends Optim. 1.3 (2014), pp. 127–239.
[PBM] Lawrence Page, Sergey Brin, Rajeev Motwani, and Terry Winograd. The PageRank Citation Ranking: Bringing Order to the Web. Technical Report 1999-66. Stanford InfoLab, Nov. 1999.
Comments