How I Learned to Stop Worrying and Love Retraining

TL;DR: This is an informal summary of our recent ICLR2023 paper How I Learned to Stop Worrying and Love Retraining by Max Zimmer, Christoph Spiegel, and Sebastian Pokutta, in which we reassess Iterative Magnitude Pruning (IMP) [HPTD]. Recent works [RFC, LH] demonstrate how the learning rate schedule during retraining crucially influences recovery from pruning-induced model degradation. We extend these findings, proposing a linear learning rate schedule with an adaptively chosen initial value, which we find to significantly improve post-retraining performance. We also challenge commonly held beliefs of IMP’s performance and efficiency by introducing BIMP, a budgeted IMP-variant. Our study not only enhances understanding of the retraining phase, but it also questions the prevailing belief that we should strive to avoid the need for retraining.

Written by Max Zimmer.

Introduction and motivation

Modern Neural Networks are often highly over-parameterized, leading to significant memory demands and lengthy, computation-heavy training and inference processes. An effective solution to this is pruning, where (groups of) weights are zeroed out, significantly compressing the architecture at hand. The resulting sparse models require only a fraction of the storage and FLOPs but still perform comparably to their dense counterparts. However, as most compression strategies, pruning also comes with a tradeoff: a very heavily pruned model will normally be less performant than its dense counterpart.

Among the various strategies on when and which weights to prune, Iterative Magnitude Pruning (IMP) stands out due to its simplicity. Following the prune after training paradigm, IMP operates on a pretrained model: it starts from a well-converged model (or trains one from scratch) and then completes prune-retrain cycles iteratively or in a One Shot fashion. Pruning, eliminating a fraction of the smallest magnitude weights, usually reduces the network’s performance which has then to be recovered in a subsequent retraining phase. Typically, one performs as many cycles as are required to reach a desired degree of compression with each cycle consisting of pruning followed by retraining. IMP falls under the umbrella of pruning-instable algorithms: significant performance degradation occurs during pruning, necessitating a subsequent recovery phase through retraining. On the other hand, there exist pruning-stable algorithms. Such methods use techniques like regularization to strongly bias the regular training process, thereby driving convergence towards an almost sparse model. Consequently, the final ‘hard’ pruning step results in a minimal accuracy decline, effectively eliminating the need for retraining.

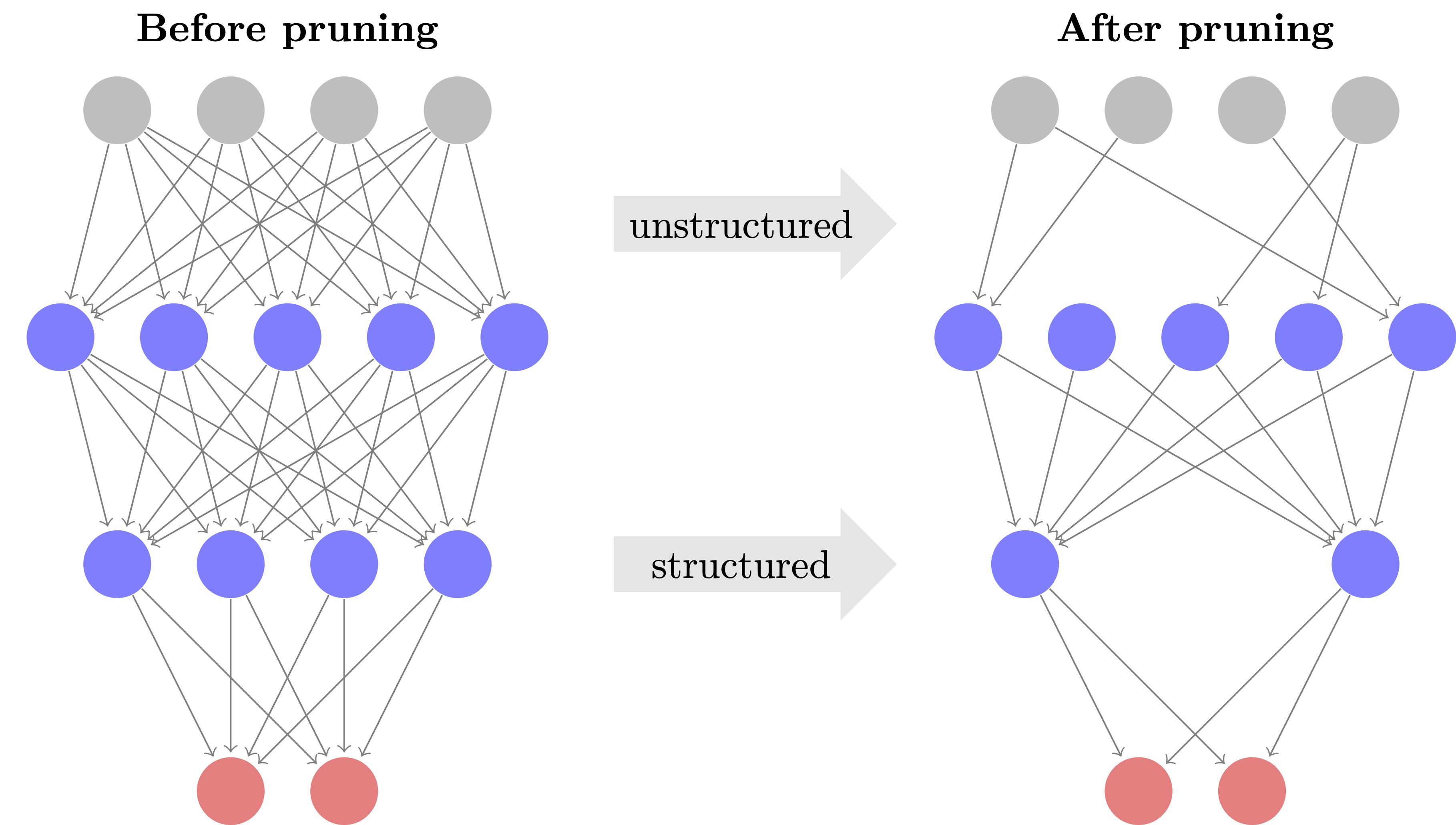
Figure 1. Pruning either removes individual weights or entire groups such as neurons.

Despite its simplicity, being straightforward to implement, modularly adjustable and requiring little computational overhead per iteration, IMP is often claimed to be inferior to pruning-stable approaches, mainly for two reasons:

1. It is said to be computationally inefficient since it requires many prune-retrain cycles. Pruning-stable approaches find a sparse solution throughout regular training, while IMP first requires training an entire dense model, followed by many cycles.
2. It is said to achieve sub-optimal sparsity-accuracy-tradeoffs since it employs ‘hard’ pruning instead of ‘learning’ the sparsity pattern throughout training.

In our work, we challenge these beliefs. We begin by analyzing how to obtain empirically optimal performance in the retraining phase by leveraging an appropriate learning rate schedule.

Improving the retraining phase

To perform retraining, we need to choose a learning rate schedule. To that end, let \((\eta_t)_{t\leq T}\) be the learning rate schedule of original training for \(T\) epochs and let \(T_{rt}\) be the number of retraining epochs, where we assume that \(\max_{t \leq T}\eta_t = \eta_1\) and the learning rate is decaying over time, as is typically the case. Previous works have proposed several different retraining schedules:

• Finetuning (FT, [HPTD]): Use the last learning rate \(\eta_T\) for all retraining epochs.
• Learning Rate Rewinding (LRW, [RFC]): Rewind the learning rate to epoch \(T-T_{rt}\).
• Scaled Learning Rate Restarting (SLR, [LH]): Proportionally compress the original schedule to fit the \(T_{rt}\) training epochs.
• Cyclic Learning Rate Restarting (CLR, [LH]): Use a 1-cycle cosine decay schedule starting from \(\eta_1\).

While gradually improving upon their respective predecessor, we believe that these specific heuristics lack comprehensive context for their individual contributions to enhancing the retraining phase. We think that first and foremost, these findings should be interpreted in the context of Budgeted Training by Li et al. [LYR], who empirically determine optimal learning rate schedules given training for a fixed number of iterations and not until convergence as is commonly assumed. Remarkably, their findings closely resemble the development and improvement of FT, LRW, SLR and CLR. Further, Li et al. find that a linear schedule works best.

With that in mind, we hypothesize and demonstrate that these findings transfer to the retraining phase after pruning, proposing to leverage a linearly decaying schedule (\(\eta_1 \rightarrow 0\)), which we call Linear Learning Rate Restarting (LLR). Figure 1 illustrates the different schedules on a toy example.

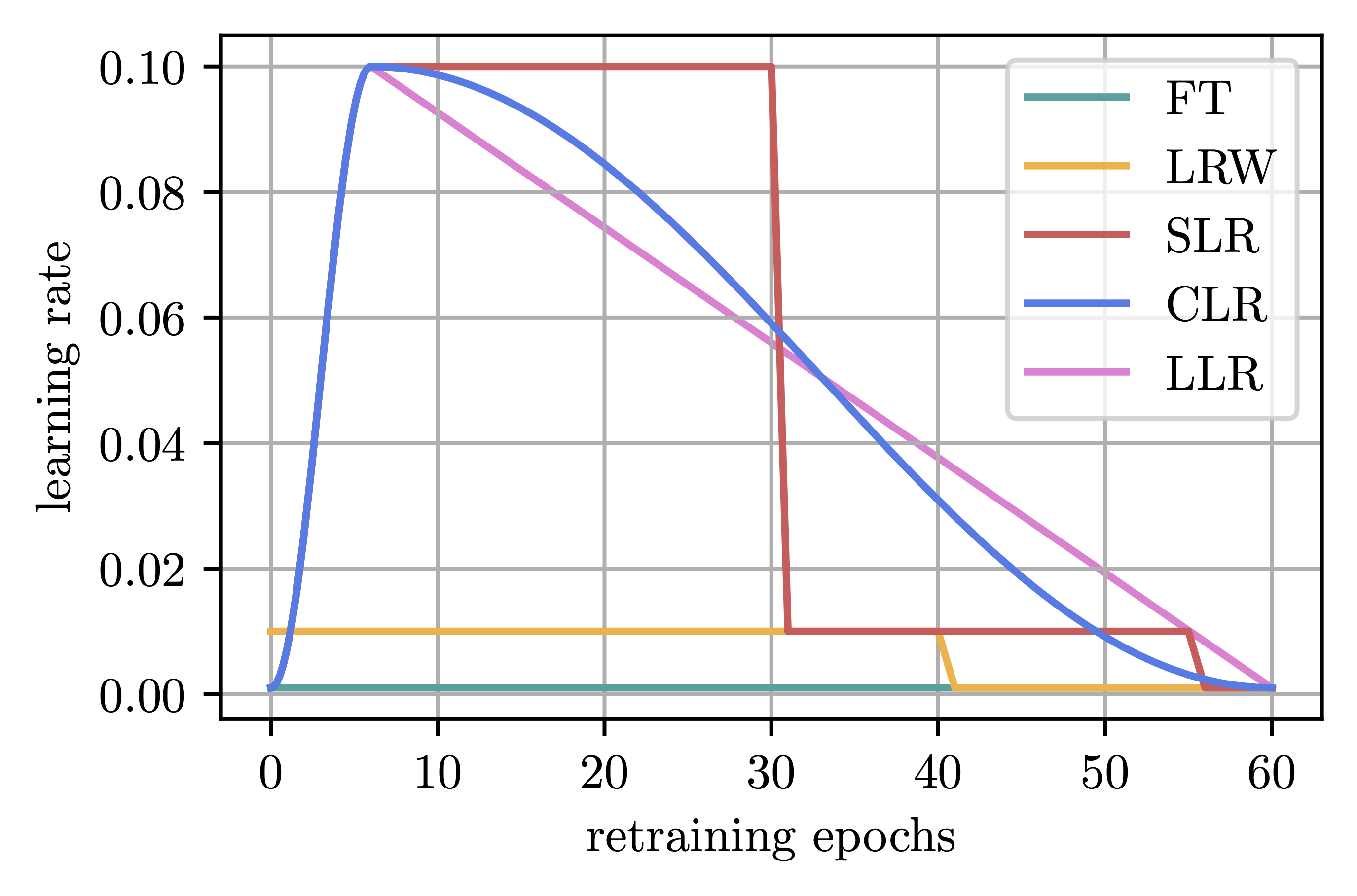
Figure 2. Different retraining schedules, assuming a stepped schedule during pretraining.

Typically, the number of retraining epochs is much smaller than the length of original training, i.e., \(T_{rt} \ll T\), and it is thus unclear whether re-increasing the learning rate to the largest value \(\eta_1\) is desirable, given a potentially too short amount of time to recover such an aggressive restarting of the learning rate. LRW implicitly deals with this problem by coupling the magnitude of the initial learning rate to the retraining length \(T_{rt}\). Furthermore, pruning either 20% or 90% differently disrupts the model, leading to different degrees of loss increase. We hence hypothesize that the learning rate should also reflect the magnitude of pruning impact. With larger pruning-induced losses, quicker recovery may be achieved by taking bigger steps towards the optimum. Conversely, for minor performance degradations, taking too large steps could potentially overshoot a nearby optimum.

Addressing these issues, we propose Adaptive Linear Learning Rate Restarting (ALLR), which leverages the empirically-optimal linear schedule but adaptively discounts the initial value of the learning rate by a factor \(d \in [0,1]\) to account for both the available retraining time and the performance drop induced by pruning, instead of relying on \(\eta_1\) as a one-fits-all solution. ALLR achieves this goal by first measuring the relative \(L_2\)-norm change in the weights due to pruning, that is after pruning an \(s \in \left( 0, 1 \right]\) fraction of the remaining weights, we compute the normalized distance between the weight vector \(\theta\) and its pruned version \(\theta^p\) in the form of

\begin{equation} d_1 = \frac{\Vert \theta - \theta^p \Vert_2}{\Vert \theta \Vert_2\cdot \sqrt{s}} \in [0,1], \end{equation}

where normalization by \(\sqrt{s}\) ensures that \(d_1\) can actually attain the full range of values in \([0,1]\). We then determine \(d_2 = T_{rt} / T\) to account for the length of the retrain phase and choose \(d \cdot \eta_1\) as the initial learning rate for ALLR where \(d = \max (d_1, d_2)\).

The table below shows part of the results of the effectiveness of ALLR given ResNet-50 trained on ImageNet. ALLR is able to outperform previous approaches, often by a large margin and across a wide variety of retraining budgets and target sparsities. Please see the full paper for extensive results on image classification, semantic segmentation and neural machine translation tasks and architectures, furthermore including results for structured pruning.

Table 1. ResNet-50 on ImageNet: Performance of the different learning rate translation schemes for One Shot IMP for target sparsities of 70%, 80% and 90% and retrain times of 2.22% (2 epochs), 5.55% (5 epochs) and 11.11% (10 epochs) of the initial training budget. Results are averaged over two seeds with the standard deviation indicated. The first, second, and third best values are highlighted.

Challenging commonly held beliefs about IMP

Having established that we can recover pruning-induced losses more effectively by taking proper care of the learning rate, we return to the two drawbacks of IMP when compared to pruning-stable methods, which as opposed to IMP are able to produce a sparse model starting from random initialization without needing further retraining. To verify whether the claimed disadvantages of IMP are backed by evidence, we propose Budgeted IMP (BIMP), where the same lessons we previously derived from Budgeted Training for the retraining phase of IMP are applied to the initial training of the network. Given a budget of \(T\) epochs, BIMP simply trains a network for some \(T_0 < T\) epochs using a linear schedule and then applies IMP with ALLR on the output for the remaining \(T-T_0\) epochs. BIMP obtains a pruned model from scratch within the same budget as pruning-stable methods, while still maintaining the key characteristics of IMP, i.e.,

• we prune ‘hard’ and do not allow weights to recover in subsequent steps, and
• we do not impose any particular additional implicit bias during either training or retraining.

The following table compares BIMP to a variety of pruning-stable methods trained on CIFAR-10 (above) and ImageNet (below), given three different levels of sparsity. Despite inheriting the properties of IMP, we find that BIMP reaches results on-par to or better than much more complex methods. Further, our experiments show that BIMP is among the most efficient approaches as measured by the number of images processed per training iteration (second column).

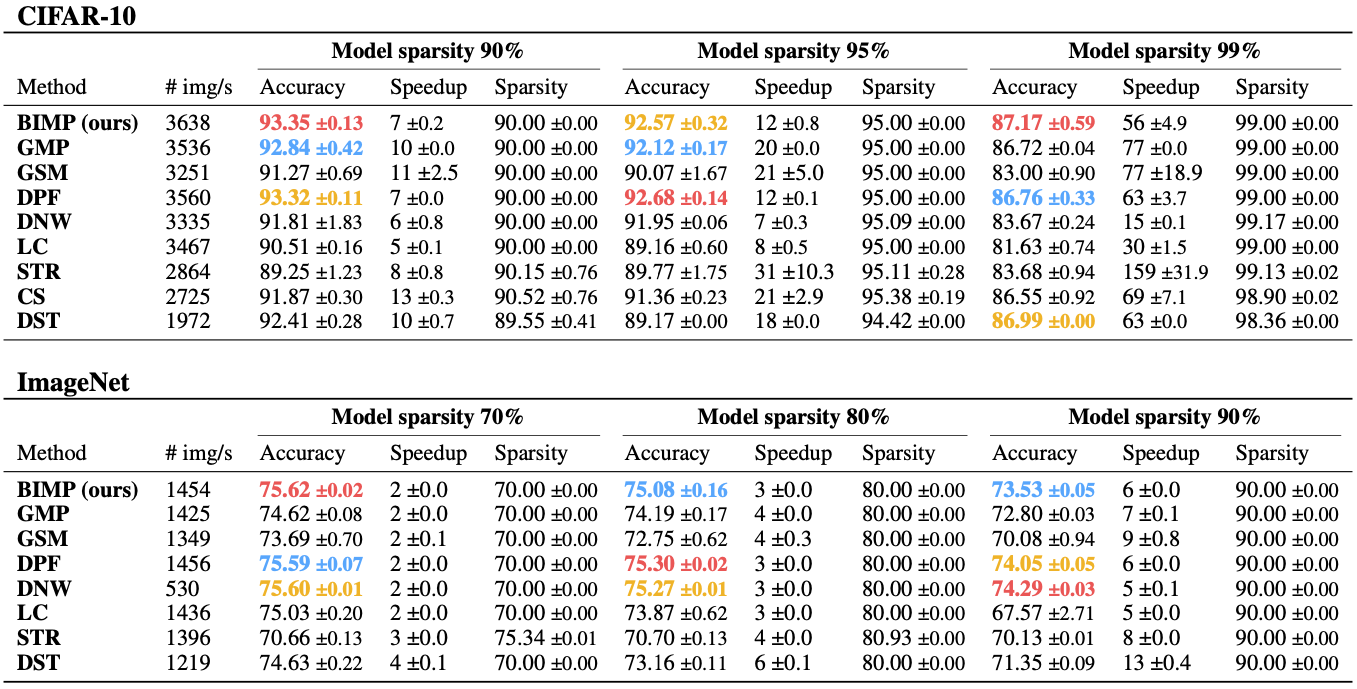
Table 2. ResNet-56 on CIFAR-10 (above) and ResNet-50 on ImageNet (below): Comparison between BIMP and pruning-stable methods when training for goal sparsity levels of 90%, 95%, 99% (CIFAR-10) and 70%, 80%, 90% (ImageNet), denoted in the main columns. Each subcolumn denotes the Top-1 accuracy, the theoretical speedup and the actual sparsity achieved by the method. Further, we denote the images-per-second throughput during training, i.e., a higher number indicates a faster method. All results are averaged over multiple seeds and include standard deviations. The first, second, and third best values are highlighted.

Conclusion

Contrary to the prevailing notion of IMP’s inferiority, our work reveals that when the learning rate is appropriately managed, this arguably simplest sparsification approach can outperform much more complex methods in terms of both performance and efficiency. Further, we put the development and benefits of different retraining schedules into perspective and provide a strong alternative with ALLR. However, let us emphasize that the goal of our work was not to suggest yet another acronym and claim it to be the be-all and end-all of network pruning, but rather to emphasize that IMP can serve as a strong, easily implemented, and modular baseline, which should be considered before suggesting further convoluted novel methods.

You can find the paper on arXiv. Our code is publicly available on GitHub. Please also check out our ICLR2023 poster and SlidesLive presentation for more information.

References

[HPTD] Song Han, Jeff Pool, John Tran, and William Dally. Learning both weights and connections for efficient Neural Networks. In C. Cortes, N. Lawrence, D. Lee, M. Sugiyama, and R. Garnett (eds.), Advances in Neural Information Processing Systems, volume 28. Curran Associates, Inc., 2015. pdf

[LH] Duong Hoang Le and Binh-Son Hua. Network pruning that matters: A case study on retraining variants. In International Conference on Learning Representations, 2021. pdf

[LYR] Mengtian Li, Ersin Yumer, and Deva Ramanan. Budgeted training: Rethinking deep neural network training under resource constraints. In International Conference on Learning Representations, 2020. pdf

[RFC] Alex Renda, Jonathan Frankle, and Michael Carbin. Comparing rewinding and fine-tuning in neural network pruning. In International Conference on Learning Representations, 2020. pdf