TL;DR: This is an informal discussion of our recent paper Acceleration of Frank-Wolfe algorithms with open loop step-sizes by Elias Wirth, Thomas Kerdreux, and Sebastian Pokutta. In the paper, we study accelerated convergence rates for the Frank-Wolfe algorithm (FW) with open loop step-size rules, characterize settings for which FW with open loop step-size rules is non-asymptotically faster than FW with line search or short-step, and provide a partial answer to an open question in kernel herding.

Written by Elias Wirth.

Introduction and motivation

Frank-Wolfe algorithms (FW) [F], see Algorithm 1, are popular first-order methods to solve convex constrained optimization problems of the form

\[\min_{x\in \mathcal{C}} f(x),\]

where $\mathcal{C}\subseteq\mathbb{R}^d$ is a compact convex set and $f\colon \mathcal{C} \to \mathbb{R}$ is a convex and smooth function. FW and its variants rely on a linear minimization oracle instead of potentially expensive projection-like oracles. Many works have identified accelerated convergence rates under various structural assumptions on the optimization problem and for specific FW variants when using line search or short-step, requiring feedback from the objective function, see, e.g., [GH13, GH15, GM, J, LJ] for an incomplete list of references.


Algorithm 1. Frank-Wolfe algorith (FW) [F]

Input: Starting point $x_0\in\mathcal{C}$, step-size rule $\eta_t \in [0, 1]$.
$\text{ }$ 1: $\text{ }$ for $t=0$ to $T$ do
$\text{ }$ 2: $\quad$ $p_t\in \mathrm{argmin}_{p\in \mathcal{C}} \langle \nabla f(x_t), p - x_t\rangle$
$\text{ }$ 3: $\quad$ $x_{t+1} \gets (1-\eta_t) x_t + \eta_t p_t$
$\text{ }$ 4: $\text{ }$ end for


However, little is known about accelerated convergence regimes utilizing open loop step-size rules, a.k.a. FW with pre-determined step-sizes, which are algorithmically extremely simple and stable. In our paper, most of the open loop step-size rules are of the form

\[\eta_t = \frac{4}{t+4}.\]

One of the main motivations for studying FW with open loop step-size rules is an unexplained phenomenon in kernel herding: In the right plot of Figure 3 of [BLO], the authors observe that FW with open loop step-size rules converges at the optimal rate [BLO] of $\mathcal{O}(1/t^2)$, whereas FW with line search or short-step converges at a rate of $\Omega(1/t)$. For this setting, FW with open loop step-size rules converges at the optimal rate, whereas FW with line search or short-step converge at a suboptimal rate. Despite substantial research interest in the connection between FW and kernel herding, so far, this behaviour remained unexplained.

However, kernel herding is not the only problem setting for which FW with open loop step-size rules can converge faster than FW with line search or short-step. In [B], the author proves that when the feasible region is a polytope, the objective function is strongly convex, the optimum lies in the interior of an at least one-dimensional face of the feasible region $\mathcal{C}$, and some other mild assumptions are satisfied, FW with open loop step-size rules asymptotically converges at a rate of $\mathcal{O}(1/t^2)$. Combined with the convergence rate lower bound of $\Omega(1/t^{1+\epsilon})$ for any $\epsilon > 0$ for FW with line search or short-step [W], this characterizes a setting for which FW with open loop step-size rules converges asymptotically faster than FW with line search or short-step.

Contributions

The main goal of the paper is to address the current gaps in our understanding of FW with open loop step-size rules.

1. Accelerated rates depending on the location of the unconstrained optimum. For FW with open loop step-size rules, the primal gap does not decay monotonously, unlike for FW with line search or short-step. We thus derive a different proof template that captures several of our acceleration results: For FW with open loop step-size rules, we derive convergence rates of up to $\mathcal{O}(1/t^2)$

  1. when the feasible region is uniformly convex and the optimum lies in the interior of the feasible region,
  2. when the objective satisfies a Hölderian error bound (think, relaxation of strong convexity) and the optimum lies in the exterior of the feasible region,
  3. and when the feasible region is uniformly convex and the objective satisfies a Hölderian error bound.

2. FW with open loop step-size rules can be faster than with line search or short-step. We derive a non-asymptotic version of the accelerated convergence result in [B]. More specifically, we show that when the feasible region is a polytope, the optimum lies in the interior of an at least one-dimensional face of $\mathcal{C}$, the objective is stronly convex, and some additional mild assumptions are satisfied, FW with open loop step-size rules converges at a non-asymptotic rate of $O(1/t^2)$. Combined with the convergence rate lower bound for FW with line search or short-step [W], we thus characterize problem instances for which FW with open loop step-size rules converges non-asymptotically faster than FW with line search or short-step.

fig1 fig2

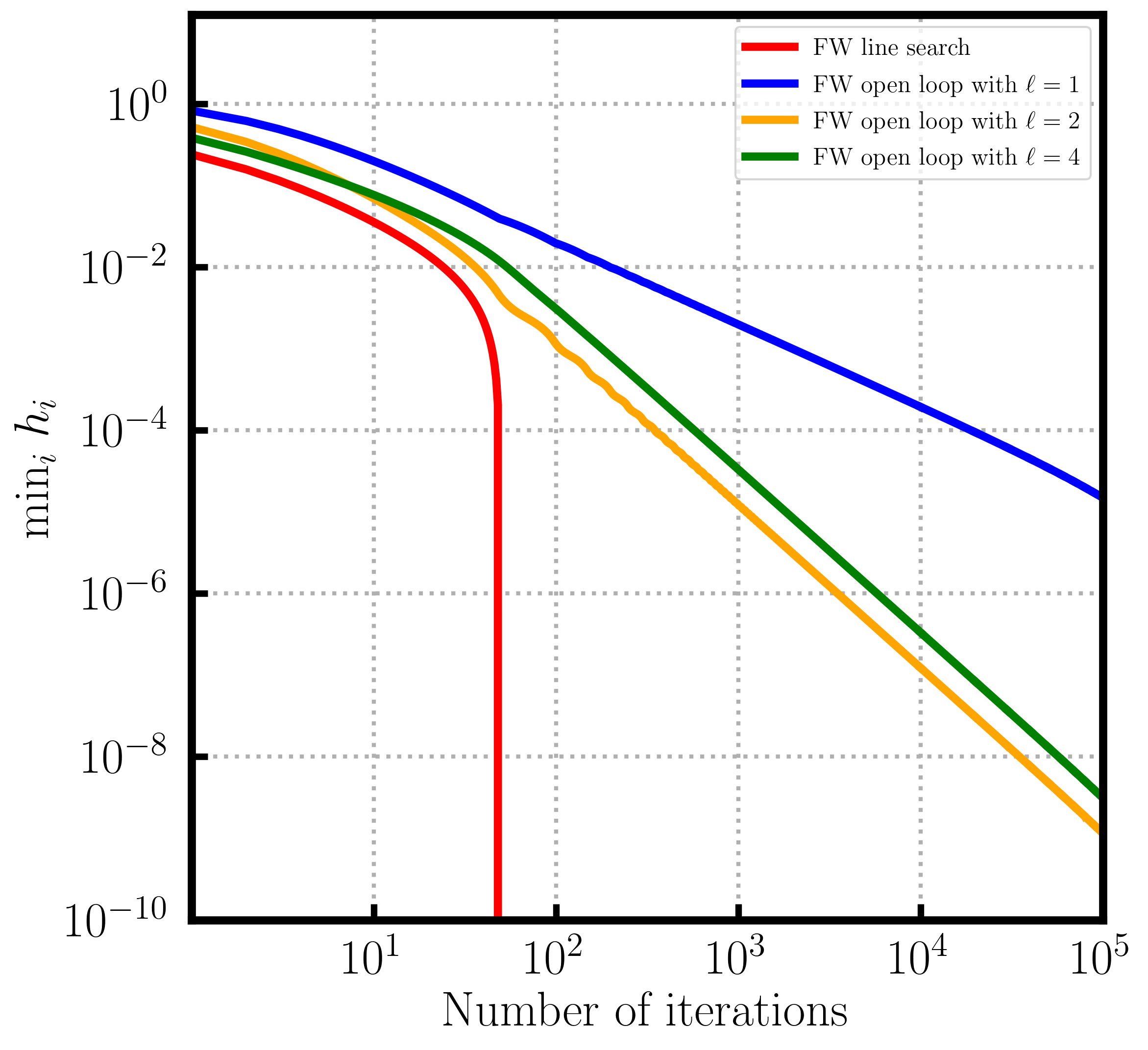
Figure 1. Convergence over probability simplex. Depending on the position of the contrained optimum line search (left) can be slower than open loop or (right) faster than open loop.

3. Algorithmic variants. When the feasible region is a polytope, we also study FW variants that were traditionally used to overcome the convergence rate lower bound [W] for FW with line search or short-step. Specifically, we present open loop versions of the Away-Step Frank-Wolfe algorithm (AFW) [LJ] and the Decomposition-Invariant Frank-Wolfe algorithm (DIFW) [GH13]. For both algorithms, we derive convergence rates of order $O(1/t^2)$.

4. Addressing an unexplained phenomenon in kernel herding. We answer the open problem from [BLO], that is, we explain why FW with open loop step-size rules converges at a rate of $\mathcal{O}(1/t^2)$ in the infinite-dimensional kernel herding setting of the right plot of Figure 3 in [BLO].

fig3 fig4

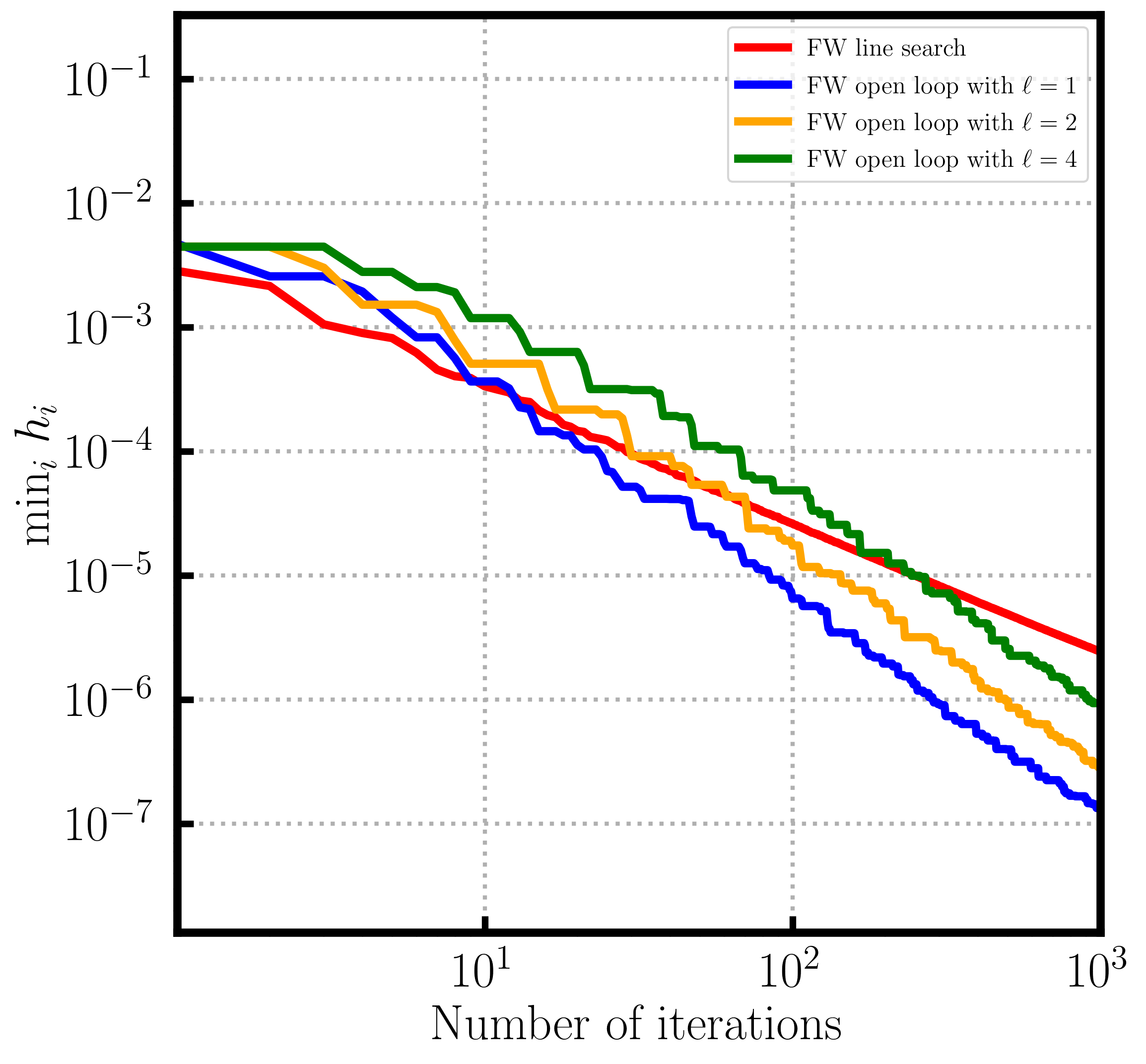
Figure 2. Kernel Herding. Open loop step sizes can outperform line search (and short step) (left) uniform (right) non-uniform case.

5. Improved convergence rate after finite burn-in. For many of our results, so as to not contradict the convergence rate lower bound of [J], the derived accelerated convergence rates only hold after an initial number of iterations, that is, the accelerated rates require a burn-in phase. This phenomenon is also referred to as accelerated local convergence [CDLP, DCP]. We study this behvaviour both in theory and with numerical experiments for FW with open loop step-size rules.

References

[B] Bach, F. (2021). On the effectiveness of richardson extrapolation in data science. SIAM Journal on Mathematics of Data Science, 3(4):1251–1277.

[BLO] Bach, F., Lacoste-Julien, S., and Obozinski, G. (2012). On the equivalence between herding and conditional gradient algorithms. In ICML 2012 International Conference on Machine Learning.

[CDLP] Carderera, A., Diakonikolas, J., Lin, C. Y., and Pokutta, S. (2021a). Parameter-free locally accelerated conditional gradients. arXiv preprint arXiv:2102.06806.

[DCP] Diakonikolas, J., Carderera, A., and Pokutta, S. (2020). Locally accelerated conditional gradients. In International Conference on Artificial Intelligence and Statistics, pages 1737–1747. PMLR.

[F] Frank, M., Wolfe, P., et al. (1956). An algorithm for quadratic programming. Naval research logistics quarterly, 3(1-2):95–110

[GH13] Garber, D. and Hazan, E. (2013). A linearly convergent conditional gradient algorithm with applications to online and stochastic optimization. arXiv preprint arXiv:1301.4666.

[GH15] Garber, D. and Hazan, E. (2015). Faster rates for the frank-wolfe method over strongly-convex sets. In International Conference on Machine Learning, pages 541–549. PMLR.

[GM] Guélat, J. and Marcotte, P. (1986). Some comments on wolfe’s ‘away step’. Mathematical Programming, 35(1):110–119.

[J] Jaggi, M. (2013). Revisiting frank-wolfe: Projection-free sparse convex optimization. In International Conference on Machine Learning, pages 427–435. PMLR.

[LJ] Lacoste-Julien, S. and Jaggi, M. (2015). On the global linear convergence of frank-wolfe optimization variants. Advances in Neural Information Processing Systems, 28:496–504.

[W] Wolfe, P. (1970). Convergence theory in nonlinear programming. Integer and nonlinear programming, pages 1–36.