Second-order Conditional Gradient Sliding

TL;DR: This is an informal summary of our recent paper Second-order Conditional Gradient Sliding by Alejandro Carderera and Sebastian Pokutta, where we present a second-order analog of the Conditional Gradient Sliding algorithm [LZ] for smooth and strongly-convex minimization problems over polytopes. The algorithm combines Inexact Projected Variable-Metric (PVM) steps with independent Away-step Conditional Gradient (ACG) steps to achieve global linear convergence and local quadratic convergence in primal gap. The resulting algorithm outperforms other projection-free algorithms in applications where first-order information is costly to compute.

Written by Alejandro Carderera.

What is the paper about and why you might care

Consider a problem of the sort: \(\tag{minProblem} \begin{align} \label{eq:minimizationProblem} \min\limits_{x \in \mathcal{X}} f(x), \end{align}\) where $\mathcal{X}$ is a polytope and $f(x)$ is a twice differentiable function that is strongly convex and smooth. We assume that solving an LP over $\mathcal{X}$ is easy, but projecting using the Euclidean norm (or any other norm) onto $\mathcal{X}$ is expensive. Moreover, we also assume that evaluating $f(x)$ is expensive, and so is computing the gradient and the Hessian of $f(x)$. An example of such an objective function can be found when solving an MLE problem to estimate the parameters of a Gaussian distribution modeled as a sparse undirected graph [BEA] (also known as the Graphical Lasso problem). Another example is the objective function used in logistic regression problems when the number of samples is high.

Projected Variable-Metric algorithms

Working with such unwieldy functions is often too expensive, and so a popular approach to tackling (minProblem) is to construct an approximation to the original function whose gradients are easier to compute. A linear approximation of $f(x)$ at $x_k$ using only first-order information will not contain any curvature information, giving us little to work with. Consider, on the other hand a quadratic approximation of $f(x)$ at $x_k$, denoted by $\hat{f_k}(x)$, that is:

\[\tag{quadApprox} \begin{align} \label{eq:quadApprox} \hat{f_k}(x) = f(x_k) + \left\langle \nabla f(x_k), x - x_k \right\rangle + \frac{1}{2} \norm{x - x_k}_{H_k}^2, \end{align}\]

where $H_k$ is a positive definite matrix that approximates the Hessian $\nabla^2 f(x_k)$. Algorithms that minimize the quadratic approximation $\hat{f}_k(x)$ over $\mathcal{X}$ at each iteration and set

\[x_{k+1} = x_k + \gamma_k (\operatorname{argmin}_{x\in \mathcal{X}} \hat{f_k}(x) - x_k)\]

for some \(\gamma_k \in [0,1]\) are dubbed Projected Variable-Metric (PVM) algorithms. These algorithms are useful when the progress per unit time obtained by moving towards the minimizer of $\hat{f}_k(x)$ over $\mathcal{X}$ at each time step is greater than the progress per unit time obtained by taking a step of any other first-order algorithm that makes use of the original function (whose gradients are very expensive to compute). We define the scaled projection of $x$ onto $\mathcal{X}$ when we measure the distance in the $H$-norm as \(\Pi_{\mathcal{X}}^{H} (y) \stackrel{\mathrm{\scriptscriptstyle def}}{=} \text{argmin}_{x\in\mathcal{X}} \norm{x - y}_{H}\). This allows us to interpret the steps taken by PVM algorithms as:

\[\tag{stepPVM} \begin{align} \label{eq:stepPVM} \operatorname{argmin}_{x\in \mathcal{X}} \hat{f_k}(x) = \Pi_{\mathcal{X}}^{H_k} \left( x_k - H_k^{-1} \nabla f(x_k) \right). \end{align}\]

These algorithms owe their name to this interpretation: at each iteration, as $H_k$ varies, we change the metric (the norm) with which we perform the scaled-projections, and we deform the negative of the gradient using this metric. The next image gives a schematic overview of a step of the PVM algorithm. The polytope $\mathcal{X}$ is depicted with solid black lines, the contour lines of the original objective function $f(x)$ are depicted with solid blue lines, and the contour lines of the quadratic approximation \(\hat{f}_k(x)\) are depicted with dashed red lines. Note that \(x_k - H_k^{-1}\nabla f(x_k)\) is the unconstrained minimizer of the quadratic approximation \(\hat{f}_k(x)\). The iterate used in the PVM algorithm to define the directions along which we move, i.e., \(\text{argmin}_{x\in \mathcal{X}} \hat{f}_k(x)\), is simply the scaled projection of that unconstrained minimizer onto \(\mathcal{X}\) using the norm \(\norm{\cdot}_{H_k}\) defined by $H_k$.

Figure 1. Minimization of $\hat{f_k}(x)$ over $\mathcal{X}$.

Note that if we set $H_k = \nabla^2 f(x_k)$ the PVM algorithm is equivalent to the Projected Newton algorithm, and if we set $H_k = I^n$, where $I^n$ is the identity matrix, the algorithm is equal to the Projected Gradient Descent algorithm. Intuitively, when $H_k$ is a good approximation to the Hessian $\nabla^2 f(x_k)$ we can expect to make good progress when moving along these directions. In terms of convergence, the PVM algorithm has a global linear convergence rate in primal gap when using an exact line search [KSJ], although with a dependence on the condition number that is worse than that of Projected Gradient Descent or the Away-step Conditional Gradient (ACG) algorithms. Moreover, the algorithm has a local quadratic convergence rate with a unit step size when close to the optimum $x^\esx$ if the matrix $H_k$ becomes a better and better approximation to $\nabla^2 f(x_k)$ as we approach $x^\esx$ (which we also assume in our theoretical results).

Second-order Conditional Gradient Sliding algorithm

Two questions arise:

1. Can we achieve a global linear convergence rate on par with that of the Away-step Conditional Gradient algorithm?
2. Solving the problem shown in (stepPVM) to optimality is often too expensive. Can we solve the problem to some $\varepsilon_k$-optimality and keep the local quadratic convergence?

The Second-order Conditional Gradient Sliding (SOCGS) algorithm is designed with these considerations in mind, providing global linear convergence in primal gap and local quadratic convergence in primal gap and distance to $x^\esx$. The algorithm couples an independent ACG step with line search with an Inexact PVM step with a unit step size. At the end of each iteration, we choose the step that provides the greatest primal progress. The independent ACG steps will ensure global linear convergence in primal gap, and the Inexact PVM steps will provide quadratic convergence. Moreover, the line search in the ACG step can be substituted with a step size strategy that requires knowledge of the $L$-smoothness parameter of $f(x)$ [PNAM].

We compute the PVM step inexactly using the (same) ACG algorithm with an exact line search, thereby making the SOCGS algorithm projection-free. As the function being minimized in the Inexact PVM steps is quadratic there is a closed-form expression for the optimal step size. The scaled projection problem is solved to $\varepsilon_k$-optimality, using the Frank-Wolfe gap as a stopping criterion, as in the Conditional Gradient Sliding (CGS) algorithm [LZ]. The CGS algorithm uses the vanilla Conditional Gradient algorithm to find an approximate solution to the Euclidean projection problems that arise in Nesterov’s Accelerated Gradient Descent steps. In the SOCGS algorithm, we use the ACG algorithm to find an approximate solution to the scaled-projection problems that arise in PVM steps.

Accuracy Parameter $\varepsilon_k$.

The accuracy parameter $\varepsilon_k$ in the SOCGS algorithm depends on a lower bound on the primal gap of (minProblem) which we denote by $lb\left( x_k \right)$ that satisfies $lb\left( x_k \right) \leq f\left(x_k \right) - f\left(x^\esx \right)$.

In several machine learning applications, the value of $f(x^\esx)$ is known a priori, such is the case of the approximate Carathéodory problem (see post Approximate Carathéodory via Frank-Wolfe where $f(x^\esx) = 0$). In other applications, estimating $f(x^\esx)$ is easier than estimating the strong convexity parameter (see [BTA] for an in-depth discussion). This allows for tight lower bounds on the primal gap in these cases.

If there is no easy way to estimate the value of $f(x^\esx)$, we can compute a lower bound on the primal gap at $x_k$ (bounded away from zero) using any CG variant that monotonically decreases the primal gap. It suffices to run an arbitrary number of steps $n \geq 1$ of the aforementioned variant to minimize $f(x)$ starting from $x_k$, resulting in $x_k^n$. Simply noting that $f(x_k^n) \geq f(x^\esx)$ allows us to conclude that $f(x_k) - f(x^\esx) \geq f(x_k) - f(x_k^n)$, and therefore a valid lower bound is $lb\left( x_k \right) = f(x_k) - f(x^n_k)$. The higher the number of CG steps performed from $x_k$, the tighter the resulting lower bound will be.

Complexity Analysis

For the complexity analysis, we assume that we have at our disposal the tightest possible bound on the primal gap, which is $lb\left( x_k \right) = f(x_k) - f(x^\esx)$. A looser lower bound increases the number of linear minimization calls but does not increase the number of first-order, or approximate Hessian oracle calls. As in the classical analysis of Projected Newton algorithms, after a finite number of iterations independent of the target accuracy $\varepsilon$ (which in our case are linearly convergent in primal gap) the algorithm enters a regime of quadratic convergence in primal gap. Once in this phase the algorithm requires $\mathcal{O}\left( \log(1/\varepsilon) \log(\log 1/\varepsilon)\right)$ calls to a linear minimization oracle, and $\mathcal{O}\left( \log(\log 1/\varepsilon)\right)$ calls to a first-order and approximate Hessian oracle to reach an $\varepsilon$-optimal solution.

If we were to solve problem (minProblem) using the Away-step Conditional Gradient algorithm we would need $\mathcal{O}\left( \log(1/\varepsilon)\right)$ calls to a linear minimization and first-order oracle. Using the SOCGS algorithm makes sense if the linear minimization calls are not the computational bottleneck of the algorithm and the approximate Hessian oracle is about as expensive as the first-order oracle.

Computational Experiments

We compare the performance of the SOCGS algorithm with that of other first-order projection free algorithms in settings where computing first-order information is expensive (and computing Hessian information is just as expensive). We also compare the performance of our algorithm with the recent Newton Conditional Gradient algorithm [LCT] which minimizes a self-concordant function over a convex set by performing Inexact Newton steps (thereby requiring an exact Hessian oracle) using a Conditional Gradient algorithm to compute the scaled projections. After a finite number of iterations (independent of the target accuracy $\varepsilon$), the convergence rate of the NCG algorithm is linear in primal gap. Once inside this phase an $\varepsilon$-optimal solution is reached after $\mathcal{O}\left(\log 1/\varepsilon\right)$ exact Hessian and first-order oracle calls and $\mathcal{O}( 1/\varepsilon^{\nu})$ linear minimization oracle calls, where $\nu$ is a constant greater than one.

In the first experiment the Hessian information will be inexact (but subject to an asymptotic accuracy assumption), and so we will only compare to other first-order projection-free algorithms. In the second and third experiments, the Hessian oracle will be exact. For reference, the algorithms in the legend correspond to the vanilla Conditional Gradient (CG), the Away-step Conditional Gradient (ACG) [GM], the Lazy Away-step Conditional Gradient (ACG (L)) [BPZ], the Pairwise-step Conditional Gradient (PCG) [LJ], the Conditional Gradient Sliding (CGS) [LZ], the Stochastic Variance-Reduced Conditional Gradient (SVRCG) [HL], the Decomposition Invariant Conditional Gradient (DICG) [GM2] and the Newton Conditional Gradient (NCG) [LCT] algorithm. We also present an LBFGS version of SOCGS (SOCGS LBFGS). However note that this algorithm, while performing well, does not formally satisfy our assumptions.

Figure 2. Sparse coding over the Birkhoff polytope.

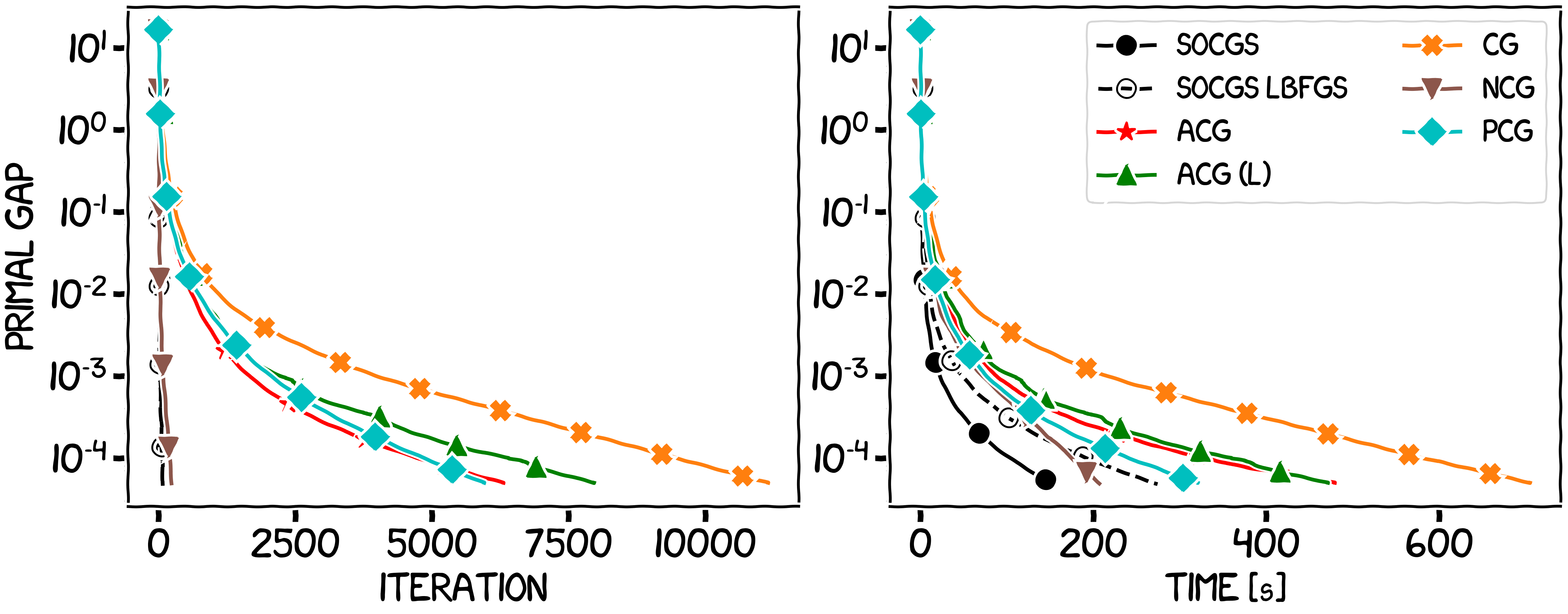
Figure 3. Inverse covariance estimation over the spectrahedron.

Figure 4. Structured logistic regression over $\ell_1$ unit ball.

References

[LZ] Lan, G., & Zhou, Y. (2016). Conditional gradient sliding for convex optimization. In SIAM Journal on Optimization 26(2) (pp. 1379–1409). SIAM. pdf

[BEA] Banerjee, O., & El Ghaoui, L. & d’Aspremont, A. (2008). Model Selection Through Sparse Maximum Likelihood Estimation for Multivariate Gaussian or Binary Data. In Journal of Machine Learning Research 9 (2008) (pp. 485–516). JMLR. pdf

[KSJ] Karimireddy, S.P., & Stich, S.U. & Jaggi, M. (2018). Global linear convergence of Newton’s method without strong-convexity or Lipschitz gradients. arXiv preprint:1806.00413. pdf

[PNAM] Pedregosa, F., & Negiar, G. & Askari, A. & Jaggi, M. (2020). Linearly Convergent Frank-Wolfe with Backtracking Line-Search. In Proceedings of the 23rd International Conference on Artificial Intelligence and Statistics. pdf

[BTA] Barré, M., & Taylor, A. & d’Aspremont, A. (2020). Complexity Guarantees for Polyak Steps with Momentum. arXiv preprint:2002.00915. pdf

[LCT] Liu, D., & Cevher, V. & Tran-Dinh, Q. (2020). A Newton Frank-Wolfe Method for Constrained Self-Concordant Minimization. arXiv preprint:2002.07003. pdf

[GM] Guélat, J., & Marcotte, P. (1986). Some comments on Wolfe’s ‘away step’. In Mathematical Programming 35(1) (pp. 110–119). Springer. pdf

[BPZ] Braun, G., & Pokutta, S. & Zink, D. (2017). Lazifying Conditional Gradient Algorithms. In Proceedings of the 34th International Conference on Machine Learning. pdf

[LJ] Lacoste-Julien, S. & Jaggi, M. (2015). On the global linear convergence of Frank-Wolfe optimization variants. In Advances in Neural Information Processing Systems 2015 (pp. 496-504). pdf

[HL] Hazan, E. & Luo, H. (2016). Variance-reduced and projection-free stochastic optimization. In Proceedings of the 33rd International Conference on Machine Learning. pdf

[GM2] Garber, D. & Meshi, O.(2016). Linear-memory and decomposition-invariant linearly convergent conditional gradient algorithm for structured polytopes. In Advances in Neural Information Processing Systems 2016 (pp. 1001-1009). pdf