Sparse Model Soups: A Recipe for Improved Pruning via Model Averaging

TL;DR: This is an informal summary of our recent paper Sparse Model Soups: A Recipe for Improved Pruning via Model Averaging by Max Zimmer, Christoph Spiegel, and Sebastian Pokutta. Recent work [WM] demonstrated that generalization performance can be significantly improved by merging multiple models fine-tuned from the same base model. However, averaging sparse models leads to a decrease in overall sparsity, due to different sparse connectivities. We discovered that by exploring a single retraining phase of Iterative Magnitude Pruning (IMP) [HPTD] with various hyperparameters, we can create models suitable for averaging while retaining the same sparse connectivity from the pruned base model. Building on this idea, we introduce Sparse Model Soups (SMS), an IMP-variant where every prune-retrain cycle starts with the averaged model from the previous phase. SMS not only maintains the sparsity pattern but also offers full modularity and parallelizability, and substantially enhances the performance of IMP.

Written by Max Zimmer.

Introduction

The field of Neural Networks has witnessed an explosion of interest over the past decade, revolutionizing numerous research and application areas by pushing the boundaries of feasibility. However, the widespread adoption of these networks is not without its challenges: Larger networks are notorious for their long training durations, extensive storage requirements, and consequently, high financial and environmental costs. Pruning, or the act of eliminating redundant parameters, serves as a valuable countermeasure to these issues. It facilitates the creation of sparse models that significantly reduce storage and floating-point operation (FLOP) demands, all while maintaining performance levels akin to their dense counterparts. A classic approach to achieve this is through Iterative Magnitude Pruning (IMP, [HPTD]), which initially trains a dense model from scratch and then iteratively prunes a fraction of the weights with smallest magnitude followed by a retraining phase to recover pruning-induced performance degradation. For a more comprehensive understanding of pruning and particularly IMP, we recommend our blogpost discussing our ICLR2023 paper How I Learned to Stop Worrying and Love Retraining.

On the other hand, diverse strategies exist that aim to enhance model performance by leveraging the combined strengths of multiple models. This ‘wisdom-of-the-crowd’ approach is typically seen in the form of prediction ensembles, where the predictions of \(m\) distinct models are collectively used to form a single, consolidated prediction. However, this method comes with a significant drawback: it requires each of the \(m\) models to be evaluated to derive a single prediction. To circumvent this efficiency hurdle, Model Soups [WM] build a single model by averaging the parameters of the \(m\) networks. This results in an inference cost that is asymptotically constant with respect to \(m\), significantly improving efficiency.

Yet, the concept of averaging multiple models isn’t without its disadvantages when contrasted with prediction ensembles. While prediction ensembles thrive on model diversity, model soups necessitate a considerable degree of similarity in the weight space. Averaging two models that are vastly dissimilar can lead the resultant model soup to land in an area of the weight space characterized by much higher loss. In fact, if two models are trained from scratch with only different random seeds, the average of their parameters will likely underperform compared to the individual models. Wortsman et al. [WM] showcase a method to create models suitable for averaging: by fine-tuning \(m\) distinct copies from a shared pre-trained base model. This approach ensures the required similarity in the weight space to create effective model soups.

A less prominent problem is that of combining multiple sparse models. Consider \(m\) different sparse models. In general, these models will have different sparse connectivities and averaging their parameters will cancel out most of the zero entries, effectively reducing the sparsity of the models and requiring to re-prune at the expense of accuracy. Figure 1 below illustrates this phenomenon.

Figure 1. Constructing the average (middle) of two networks with different sparsity pattern (left, right) can reduce the overall sparsity level, turning pruned weights (dashed) into non-zero ones (solid). Weights reactivated in the averaged model are highlighted in orange.

In this work, we address the challenge of generating models that can be averaged without disrupting their sparsity patterns. Central to our approach is the finding that conducting a single prune-retrain phase with varied hyperparameter settings such as random seed, weight decay, etc., yields models that are a) suitable for averaging, and b) retain the same sparse connectivity inherited from the original pruned base model. Building on this insight, we introduce Sparse Model Soups (SMS), a variant of IMP that commences each phase with an averaged model from the prior phase. This approach not only preserves sparse connectivity throughout the entire sparsification process, but also significantly enhances the performance of IMP.

Merging Sparse Models after One Shot pruning and Retraining

In most cases, averaging arbitrary sparse models will inadvertently reduce the sparsity level of the resulting model compared to the individual ones, potentially also compromising accuracy as these models might not be suited for averaging. However, the scenario changes when we examine models derived from a shared parent model, a technique prevalent in transfer learning [WM].

Our exploration reveals that it’s indeed feasible to average multiple models that are retrained from the same pruned base model. Here’s our approach: Consider the initial phase of the IMP process. We start with a pretrained model, prune it to achieve a desired level of sparsity, and then retrain it to compensate for the losses induced by pruning. Instead of merely retraining once, we create \(m\) copies of this pruned model and individually retrain each one under a unique hyperparameter configuration. This could involve changing factors such as the strength of weight decay or the random seed which influences the batch ordering.

When we average two (or more) models, there’s no reduction in sparsity since all models stem from the same pruned base model. Interestingly, these models are also amenable to averaging. To illustrate this, consider Figure 2 (below) where we pruned ResNet-50, pretrained on ImageNet, to 70% sparsity. We then examined all \(m \choose 2\) combinations of retrained models, plotting their maximum test accuracy on the x-axis against the test accuracy of their average on the y-axis. The results clearly show net improvements for nearly all configurations. Interestingly, merely changing the random seed led to consistent and significant performance gains of up to 1%, despite the fact that we’re averaging just two models.

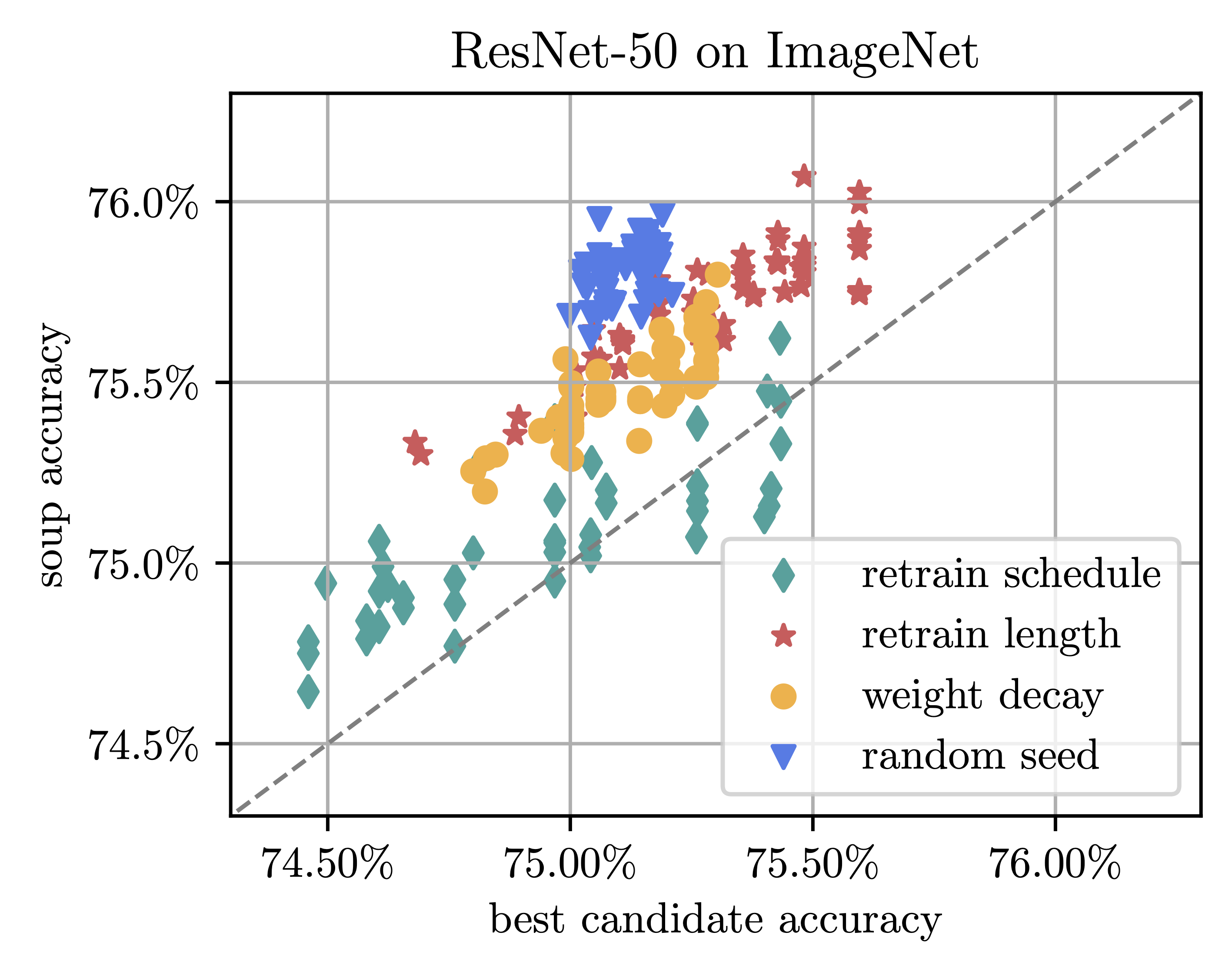
Figure 2. Accuracy of average of two models vs. the maximal individual accuracy. All models are pruned to 70% sparsity (One Shot) and retrained, varying the indicated hyperparameters.

SMS: Sparse Model Soups

Having established that the initial phase of IMP is suitable to training \(m\) models in parallel and averaging them, we’re faced with another intriguing question: Is it possible to maintain the overall sparsity while averaging models after multiple phases? Surprisingly, the answer is negative. Although models are averageable after a single prune-retrain cycle, another cycle of pruning and retraining results in models with divergent sparsity patterns: they share a common pattern after the first phase, but individual pruning leads to distinctive sparse connectivities among them.

This issue brings us to our proposed solution, the Sparse Model Soups (SMS) algorithm, as illustrated below. By capitalizing on the modularity of IMP’s phases, we construct the average model after each phase, merging \(m\) retrained models into a single model. This entity then serves as the starting point for the subsequent phase, guaranteeing that the sparsity patterns are consistent across all individual models.

Figure 4. Left: Sketch of the algorithm for a single phase and \(m=3\). Right: Pseudocode for SMS. Merge\((\cdot)\) takes \(m\) models as input and returns a linear combination of the models.

We now evaluate SMS against several critical baselines, comparing it at each prune-retrain phase with the top-performing single model amongst all candidates for averaging (best candidate). In addition, we also contrast it against the mean candidate, standard IMP (i.e., when \(m=1\)), and an enhanced variant of IMP that is retrained \(m\) times longer, which we denote as IMP+. Furthermore, we compare SMS with a method that executes standard IMP \(m\) times, then averages the models post-final phase, a strategy we call IMP-AVG. This method seeks to mitigate potential reduction in sparsity by re-pruning the model [YIN].

Table 1 outlines the results for three-phase IMP, using WideResNet-20 on CIFAR-100 and ResNet-50 on ImageNet. The left column represents the baselines, while the three central columns correspond to phases and sparsity levels, targeting 98% sparsity for CIFAR-100 and 90% for ImageNet. Each central column further breaks down into three sub-columns, indicating the number of models to average (3, 5, or 10). We observe that SMS consistently outperforms the test accuracy of the best candidate, often by a margin of 1% or more. This illustrates that the models are indeed amenable to averaging after retraining, resulting in superior generalization than individual models. SMS shows significant improvements over both the standard IMP and its extended retraining variant, IMP+, boasting up to a 2% enhancement even when employing just \(m=3\) splits.

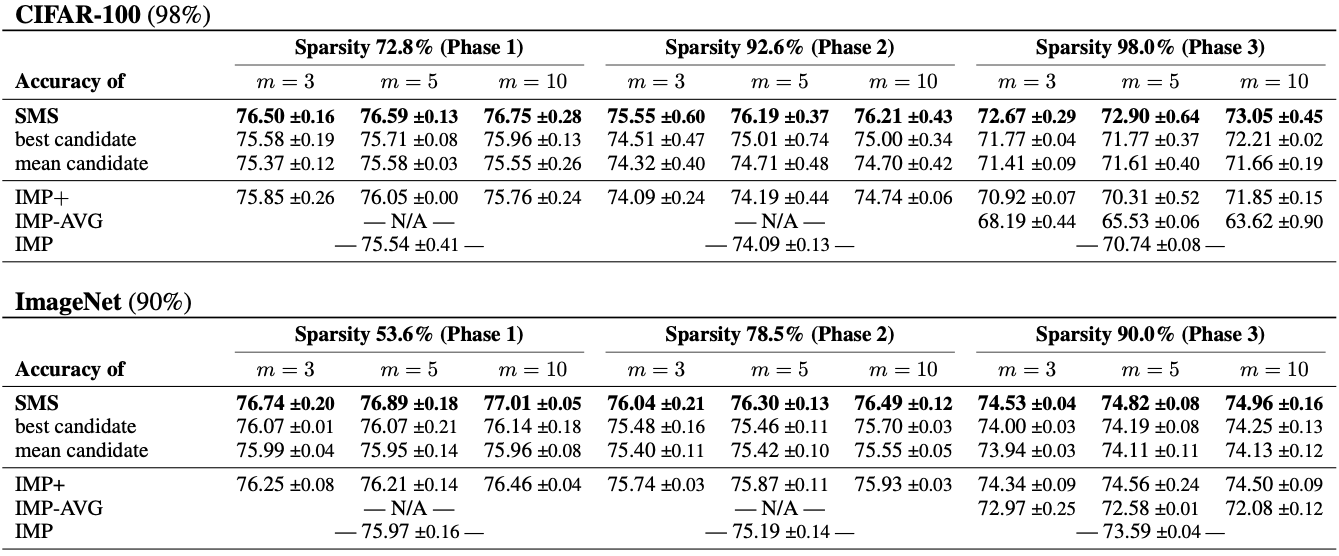
Table 1. WideResNet-20 on CIFAR-100 and ResNet-50 on ImageNet: Test accuracy comparison of SMS to several baselines for target sparsities 98% (top) and 90% (bottom) given three prune-retrain cycles. Results are averaged over multiple seeds with standard deviation included. The best value is highlighted in bold.

Conclusion

Efficient, high-performing sparse networks are crucial in resource-constrained environments. However, sparse models cannot easily leverage the benefits of parameter averaging. We addressed this issue proposing SMS, a technique that merges models while preserving sparsity, substantially enhancing IMP and outperforming multiple baselines. Please feel free to check out our paper on arXiv, where we further improve pruning during training methods such as BIMP [ZSP] and DPF [LIN] by integrating SMS. Our code is publicly available on GitHub.

References

[HPTD] Song H., Jeff P., John T., Dally W.. Learning both weights and connections for efficient Neural Networks. In C. Cortes, N. Lawrence, D. Lee, M. Sugiyama, and R. Garnett (eds.), Advances in Neural Information Processing Systems, volume 28. Curran Associates, Inc., 2015. pdf

[LIN] Lin, T., Stich, S. U., Barba, L., Dmitriev, D., & Jaggi, M. (2020). Dynamic model pruning with feedback. arXiv preprint arXiv:2006.07253. pdf

[WM] Wortsman, Mitchell, et al. “Model soups: averaging weights of multiple fine-tuned models improves accuracy without increasing inference time.” International Conference on Machine Learning. PMLR, 2022. pdf

[YIN] Yin, L., Menkovski, V., Fang, M., Huang, T., Pei, Y., & Pechenizkiy, M. (2022, August). Superposing many tickets into one: A performance booster for sparse neural network training. In Uncertainty in Artificial Intelligence (pp. 2267-2277). PMLR. pdf

[ZSP] Zimmer, M., Spiegel, C., & Pokutta, S. (2022, September). How I Learned to Stop Worrying and Love Retraining. In The Eleventh International Conference on Learning Representations. pdf