Projection-Free Optimization on Uniformly Convex Sets
TL;DR: This is an informal summary of our recent paper Projection-Free Optimization on Uniformly Convex Sets by Thomas Kerdreux, Alexandre d’Aspremont, and Sebastian Pokutta. We present convergence analyses of the Frank-Wolfe algorithm in settings where the constraint sets are uniformly convex. Our results generalize different analyses of [P], [DR], [D], and [GH] when the constraint sets are strongly convex. For instance, the $\ell_p$ balls are uniformly convex for all $p > 1$, but strongly convex for $p\in]1,2]$ only. We show in these settings that uniform convexity of the feasible region systematically induces accelerated convergence rates of the Frank-Wolfe algorithm (with short steps or exact line-search). This shows that the Frank-Wolfe algorithm is not just adaptive to the sharpness of the objective [KDP] but also to the feasible region.
Written by Thomas Kerdreux.
We consider the following constrained optimization problem
\[\underset{x\in\mathcal{C}}{\text{argmin}} f(x),\]where $f$ is a $L$-smooth convex function and $\mathcal{C}$ is a compact convex set in a Hilbert space. Frank-Wolfe algorithms form a classical family of first-order iterative methods for solving such problems. Each iteration requires in the worst case the solution of a linear minimization problem over the original feasible domain, a subset of the domain, or a reasonable modification of the domain, i.e. a change that does not implicitly amount to a proximal operation.
The understanding of the convergence rates of Frank-Wolfe algorithms in a variety of settings is an active field of research. For smooth constrained problems, the vanilla Frank-Wolfe algorithm (FW) enjoys a tight sublinear convergence rate of $\mathcal{O}(1/T)$ (see e.g., [J] for an in-depth discussion). There are known accelerated convergence regimes, as a function of the feasible region, only when $\mathcal{C}$ is a polytope or a strongly convex set.
Frank-Wolfe Algorithm
Input: Start with $x_0 \in \mathcal{C}$, $L$ upper bound on the Lipschitz constant.
Output: Sequence of iterates $x_t$
For $t=0, 1, \ldots, T $ do:
$\qquad v_t \leftarrow \underset{v\in\mathcal{C}}{\text{argmax }} \langle -\nabla f(x_t); v - x_t\rangle$ $\qquad \triangleright $ FW vertex
$\qquad \gamma_t \leftarrow \underset{\gamma\in[0,1]}{\text{argmin }} \gamma \langle \nabla f(x_t); v_t - x_t \rangle + \frac{\gamma^2}{2} L \norm{v_t - x_t}^2$ $\qquad \triangleright$ Short step
$\qquad x_{t+1} \leftarrow (1 - \gamma_t)x_{t} + \gamma_t v_{t}$ $\qquad \triangleright$ Convex update
When $\mathcal{C}$ is a strongly convex set and \(\text{inf}_{x\in\mathcal{C}}\norm{\nabla f(x)}_\esx > 0\), FW enjoys linear convergence rates [P, DR]. Recently, [GH] showed that the Frank-Wolfe algorithm converges in \(\mathcal{O}(1/T^2)\) when the objective function is strongly convex without restriction on the position of the optimum $x^\esx$. Importantly, the conditioning of this sub-linear rate does not depend on the distance of the constrained optimum $x^\esx$ either from the boundary or the unconstrained optimum, as it is the case in [P, DR], or [GM] when the optimum $x^\esx$ is in the interior of $\mathcal{C}$. Note that all these analyses require short steps as step-size rule (or even stronger conditions such as line-search).
Finally, when $\mathcal{C}$ is a polytope and $f$ is strongly convex, corrective variants of Frank-Wolfe were recently shown to enjoy linear convergence rates, see [LJ]. No accelerated convergence rates are known for constraint sets that are neither polytopes nor strongly convex sets. We show here that uniformly convex sets, which non-trivially subsume strongly convex sets, systematically enjoy accelerated convergence rate in the respective settings of [P,DR], [GH], and [D].
Uniformly Convex Sets
A closed set $\mathcal{C}\subset\mathbb{R}^d$ is $(\alpha, q)$-uniformly convex with respect to a norm $\norm{\cdot}$, if for any $x,y\in\mathcal{C}$, any $\eta\in[0,1]$, and any $z\in\mathbb{R}^d$ with $\norm{z} = 1$, we have
\[\tag{1} \eta x + (1-\eta)y + \eta (1 - \eta ) \alpha ||x-y||^q z \in \mathcal{C}.\]At a high-level, this property is a global quantification of the set curvature that subsumes strong convexity. There exist others equivalent definitions, see e.g. [GI] in the strongly convex case. In finite-dimensional spaces, the $\ell_p$ balls form classical and important examples of uniformly convex sets. For $0 < p < 1$, the $\ell_p$ balls are non-convex. For $p\in ]1,2]$, the $\ell_p$ balls are strongly convex (or $(\alpha,2)$-uniformly convex) and $p$-uniformly convex (but not strongly convex) for $p>2$. The $p$-Schatten norms with $p>1$ or various group norms are also typical examples.
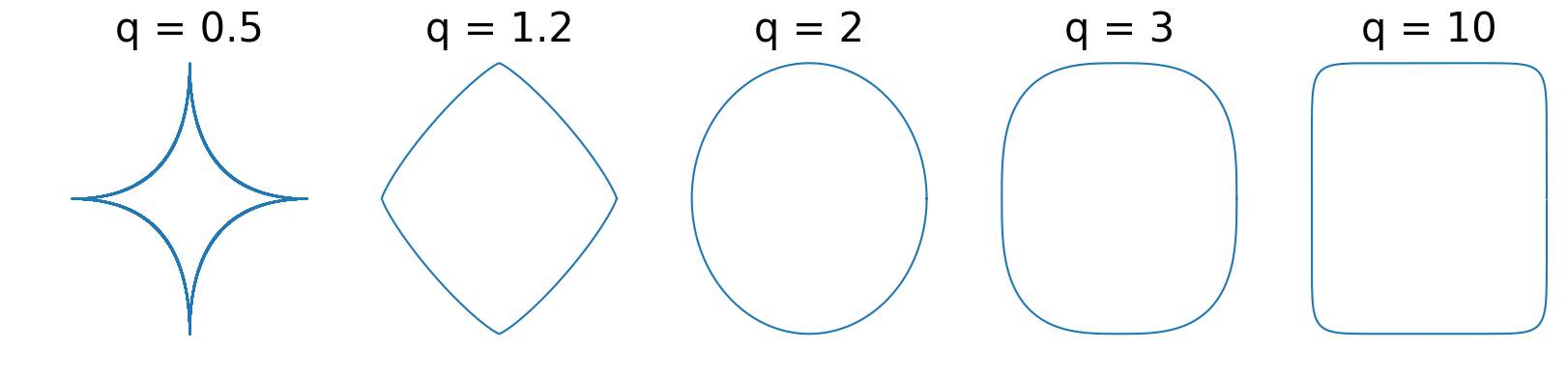
Figure 1. Example of $\ell_q$ balls.
Besides the quantification in (1), uniform convexity is a very classical notion in the study of normed spaces. Indeed, it allows to refine the convex characterization of these spaces’ unit balls, leading to a plethora of interesting properties. For instance, the various uniform convexity types of Banach spaces have consequences, notably in learning theory [DDS], online learning [ST], or concentration inequalities [JN]. Here, we show that the Frank-Wolfe algorithm accelerates as a function of the uniform convexity of $\mathcal{C}$.
Convergence analysis for Frank-Wolfe with Uniformly Convex Sets
Proof Sketch
At iteration $t$, we have $x_{t+1} = x_t + \gamma_t (v_t - x_t)$ with $\gamma_t\in[0,1]$ chosen to optimize the quadratic upper-bound on $f$ implied by $L$-smoothness. Classically then, we obtain that for any $\gamma\in[0,1]$
\[\tag{2} f(x_{t+1}) - f(x^\esx) \leq f(x_t) - f(x^\esx) - \gamma \langle - \nabla f(x_t); v_t - x_t\rangle + \frac{\gamma^2}{2} L \norm{x_t - v_t}^2.\]The Frank-Wolfe gap $g_t = \langle - \nabla f(x_t); v_t - x_t\rangle\geq 0$ contributes in the primal decrease counter-balanced by the right-hand term. Informally then, uniform convexity of the set ensures that the distance of the iterate to the Frank-Wolfe vertex $\norm{v_t - x_t}$ shrinks to zero at a specific rate that depends on $g_t$. This schema illustrates that it is generally not the case when $\mathcal{C}$ is a polytope and how various type of curvature influence the shrinking of $\norm{v_t - x_t}$ to zero.
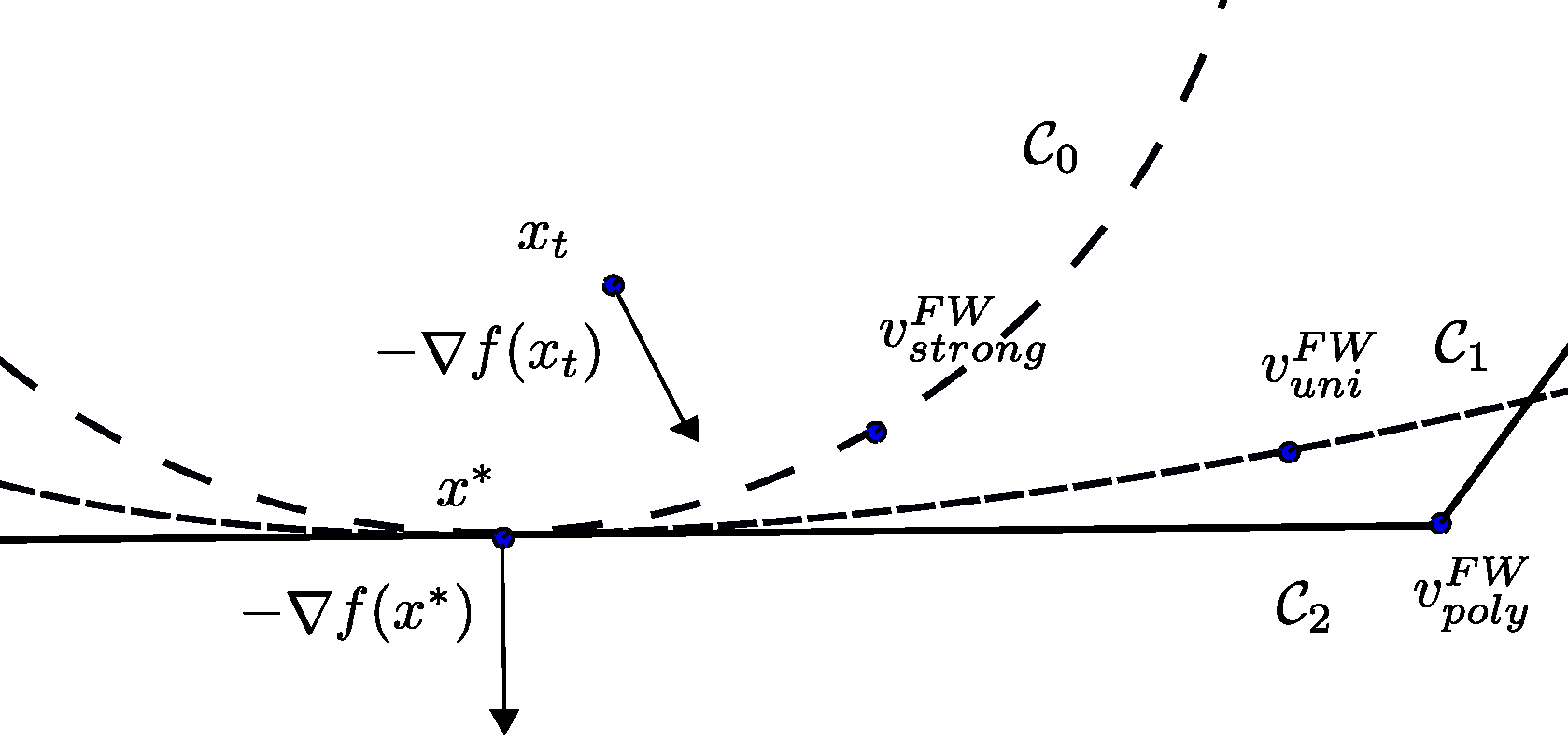
Figure 2. The uniform convexity assumption.
Scaling Inequalities
The uniform convexity parameters quantify different trade-off between the convergence to zero of $g_t$ and $\norm{v_t - x_t}$ . In particular, $(\alpha, q)$-uniform convexity of $\mathcal{C}$ implies scaling inequalities of the form \(\langle -\nabla f(x_t); v_t - x_t\rangle \geq \alpha/2 \norm{\nabla f(x_t)}_\esx \norm{v_t - x_t}^q,\) where $\norm{\cdot}_\esx$ stands for the dual norm to $\norm{\cdot}$. Plugging this scaling inequality into (1) is then the basis for the various convergence results.
Convergence results with global uniform convexity
Assuming that $\mathcal{C}$ is $(\alpha,q)$-uniformly convex and $f$ is a strongly convex and $L$-smooth function, we obtain convergence rates of $\mathcal{O}(1/T^{1/(1-1/q)})$ that interpolate between the general sub-linear rate of $\mathcal{O}(1/T)$ and the $\mathcal{O}(1/T^2)$ of [GH]. Note that we further generalize these results by relaxing the strong convexity of $f$ with $(\mu, \theta)$-Hölderian Error Bounds and the rates become $\mathcal{O}(1/T^{1/(1-2\theta/q)})$. For more details, see Theorem 2.10. of our paper or [KDP] for general error bounds in the context of the Frank-Wolfe algorithm.
Similarly, assuming \(\text{inf}_{x\in\mathcal{C}}\norm{\nabla f(x)}_\esx > 0\), when $\mathcal{C}$ is $(\alpha,q)$-uniformly convex with $q>2$, we obtain convergence rates of $\mathcal{O}(1/T^{1/(1-2/q)})$ that interpolate between the general sub-linear rate of $\mathcal{O}(1/T)$ and the linear convergence rates of [P, DR].
These two convergence regimes depend on the global uniform convexity parameters of the set $\mathcal{C}$. However, for example $\ell_3$ balls, seem to exhibit various degree of curvature depending on the position of $x^\esx$ on the boundary $\partial\mathcal{C}$.
A simple numerical experiment
We now numerically observe the convergence of Frank-Wolfe where $f$ is a quadratic and the feasible region are $\ell_p$ balls with varying $p$. We provide two different plots where we vary the position of the optimal solution $x^\esx$. In both cases we use short steps.
In the right figure, $x^\esx$ is chosen near the intersection of the $\ell_p$-balls and the half-line generated by $\sum_{i=1}^{d}e_i$, where the $(e_i)$ is the canonical basis. Informally, this corresponds to the curvy areas of the $\ell_p$ balls. On the left figure, $x^\esx$ is chosen near the intersection of the $\ell_p$ balls and the half-line generated by one of the $(e_i)$, which corresponds to a flat area for large value of $p$.
We observe that when the optimum is near a curvy area, the converge rates are asymptotically linear for $\ell_p$ balls that are not strongly convex.
| Optimum $x^\esx$ in flat area | Optimum $x^\esx$ in curvy area |
|---|---|
 |
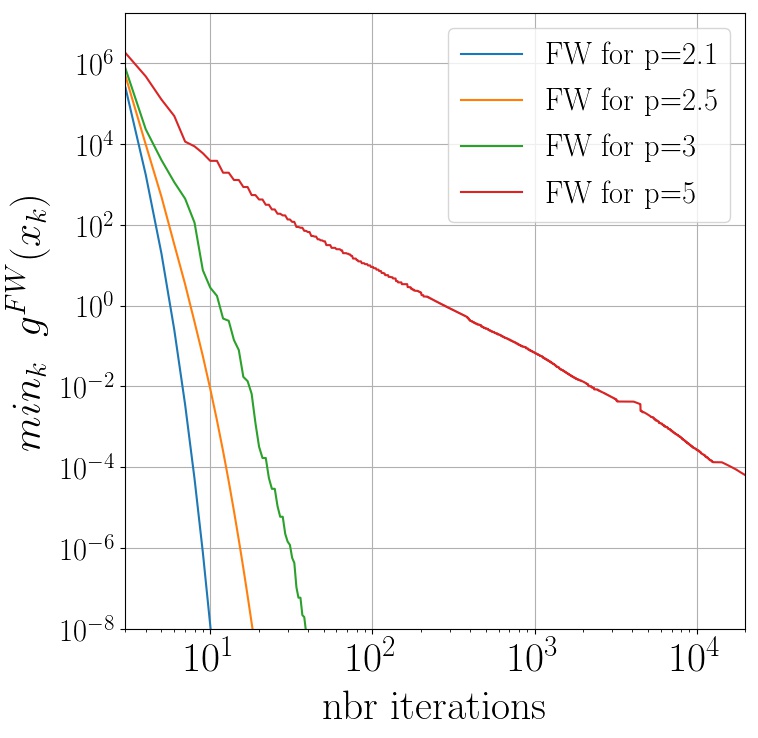 |
This suggests that the local behavior of $\mathcal{C}$ around $x^\esx$ might even better explain the convergence rates. Providing such an analysis would be in line with [D] which proves linear convergence rates assuming only local strong convexity of $\mathcal{C}$ around $x^\esx$. We extend this result to a localized notion of uniform convexity.
Frank-Wolfe Analysis with Localized Uniform Convexity
When $\mathcal{C}$ is not globally uniformly convex, the scaling inequality does not necessarily hold anymore. We rather assume the following localized version around $x^\esx$:
\[\tag{3} \langle -\nabla f(x^\esx); x^\esx - x\rangle \geq \alpha/2 \norm{\nabla f(x^\esx)}_\esx \norm{x^\esx - x}^q.\]A localized definition of uniform convexity in the form of (1) applied at $x^\esx \in \partial \mathcal{C}$ indeed implies the local scaling inequality (3). However, the local scaling inequality (3) holds in more general situations, e.g. in the case of the strong convexity analog for the local moduli of rotundity in [GI]. This condition was already identified by Dunn [D], yet without any convergence analysis as soon as $q>2$. In another blog post, we will delve into more details on the generality of (3) and related assumptions in optimization.
Assuming \(\text{inf}_{x\in\mathcal{C}} \norm{\nabla f(x)}_\esx > 0\) and a local scaling inequality at $x^\esx$ with parameters $(\alpha, q)$, we obtain convergence rates of $\mathcal{O}(1/T^{1/(1-2/(q(q-1))})$ with $q>2$ that interpolate between the general sub-linear rate of $\mathcal{O}(1/T)$ and the linear convergence rates of [D].
Note that the obtained sublinear rate via the local scaling inequality is strictly worse than the one obtained via the global scaling inequality with same $(\alpha, q)$ parameters. The sublinear rate $\mathcal{O}(1/T^{1/(1-2/(q(q-1))})$ remains however always better than $\mathcal{O}(1/T)$ when $q>2$.
Conclusion
Our results show that in all regimes (for smooth constrained problems) where the strong convexity of the constraint set is known to accelerate Frank-Wolfe algorithms (see [P, DR], [D] or [GH]), the uniform convexity of the set leads to accelerated convergence rates with respect to $\mathcal{O}(1/T)$ as well.
We also show that the local uniform convexity of $\mathcal{C}$ around $x^\esx$ already induces accelerated convergence rates. In particular, this acceleration is achieved with the vanilla Frank-Wolfe algorithm which does not require any knowledge about these underlying structural assumptions and their respective parameters. As such, our results further shed light on the adaptive properties of Frank-Wolfe type of algorithms. For instance, see also [KDP] for adaptivity with respect to error bound conditions on the objective function, or [J, LJ] for affine invariant analyses of Frank-Wolfe algorithms when the constraint set are polytopes.
References
[D] Dunn, Joseph C. Rates of convergence for conditional gradient algorithms near singular and nonsingular extremals. SIAM Journal on Control and Optimization 17.2 (1979): 187-211. pdf
[DR] Demyanov, V. F. ; Rubinov, A. M. Approximate methods in optimization problems. Modern Analytic and Computational Methods in Science and Mathematics, 1970.
[DDS] Donahue, M. J.; Darken, C.; Gurvits, L.; Sontag, E. (1997). Rates of convex approximation in non-Hilbert spaces. Constructive Approximation, 13(2), 187-220.
[GH] Garber, D.; Hazan, E. Faster rates for the frank-wolfe method over strongly-convex sets. In 32nd International Conference on Machine Learning, ICML 2015. pdf
[GI] Goncharov, V. V.; Ivanov, G. E. Strong and weak convexity of closed sets in a hilbert space. In Operations research engineering, and cyber security, pages 259–297. Springer, 2017.
[GM] Guélat, J.; Marcotte, P. (1986). Some comments on Wolfe’s ‘away step’. Mathematical Programming, 35(1), 110-119.
[HL] Huang, R.; Lattimore, T.; György, A.; Szepesvári, C. Following the leader and fast rates in linear prediction: Curved constraint sets and other regularities. In Advances in Neural Information Processing Systems, pages 4970–4978, 2016. pdf
[J] Jaggi, M. Revisiting Frank-Wolfe: Projection-free sparse convex optimization. In Proceedings of the 30th international conference on machine learning, ICML 2013. p. 427-435. pdf
[JN] Juditsky, A.; Nemirovski, A.S. Large deviations of vector-valued martingales in 2-smooth normed spaces. pdf
[KDP] Kerdreux, T.; d’Aspremont, A.; Pokutta, S. 2019. Restarting Frank-Wolfe. In The 22nd International Conference on Artificial Intelligence and Statistics (pp. 1275-1283). pdf
[LJ] Lacoste-Julien, S. ; Jaggi, Martin. On the global linear convergence of Frank-Wolfe optimization variants. In : Advances in neural information processing systems. 2015. p. 496-504. pdf
[P] Polyak, B. T. Existence theorems and convergence of minimizing sequences for extremal problems with constraints. In Doklady Akademii Nauk, volume 166, pages 287–290. Russian Academy of Sciences, 1966.
[ST] Sridharan, K.; Tewari, A. (2010, June). Convex Games in Banach Spaces. In COLT (pp. 1-13). pdf
Comments