On the unreasonable effectiveness of the greedy algorithm
TL;DR: This is an informal summary of our recent paper On the Unreasonable Effectiveness of the Greedy Algorithm: Greedy Adapts to Sharpness with Mohit Singh, and Alfredo Torrico, where we adapt the sharpness concept from convex optimization to explain the effectiveness of the greedy algorithm for submodular function maximization.
What is the paper about and why you might care
An important problem is the maximization of a non-negative monotone submodular set function $f: 2^V \rightarrow \RR_+$ subject to a cardinality constraint, i.e.,
\[\tag{maxSub} \max_{S \subseteq V, |S| \leq k} f(S).\]This problem naturally occurs in many contexts, such as, e.g., feature selection, sensor placement, and non-parametric learning. It is well known that in submodular function maximization with a single cardinality constraint we can compute a $(1-1/\mathrm{e})$-approximate solution by means of the greedy algorithm [NW], [NWF], while computing an exact solution is NP-hard. The greedy algorithm is extremely simple, selecting in each of its $k$ iterations the element with the largest marginal gain $\Delta_{S}(e) \doteq f(S \cup \setb{e}) - f(S)$:
Greedy Algorithm
Input: Non-negative, monotone, submodular function $f$ and budget $k$
Output: Set $S_g \subseteq V$
$S_g \leftarrow \emptyset$
For $i = 1, \dots, k$ do:
$\quad S_g \leftarrow S_g \cup \setb{\arg\max_{e \in V \setminus S_g} \Delta_{S_g}(e)}$
Due to its simplicity and good real-world performance the greedy algorithm is often the method of choice in large-scale tasks where more involved methods, such as, e.g., integer programming are computationally prohibitive. As mentioned before, the returned solution $S_g \subseteq V$ of the greedy algorithm satisfies [NW]
\[f(S_g) \geq (1-1/\mathrm{e}) \ f(S^\esx),\]where $S^\esx \subseteq V$ is the optimal solution to problem (maxSub).
In practice however, we often observe that the greedy algorithm performs much better than this conservative approximation guarantee suggests and several concepts such as, e.g., curvature [CC] or stability [CRV] have been proposed as a means to explain the excess performance of the greedy algorithm beyond this worst-case bound. The reason one might be interested in this, beyond understanding greedy’s performance as a function of additional properties of $f$ (which is interesting in its own right), is that the problem instance of interest might be amenable to pre-processing in order to improve conditioning with respect to these additional structural properties and hence performance.
Our results
We focus on giving an alternative explanation for those instances in which the optimal solution clearly stands out over the rest of feasible solutions. For this, we consider the concept of sharpness initially introduced in continuous optimization (see [BDL] and references contained therein) and we adapt it to submodular optimization. In convex optimization, roughly speaking, sharpness measures the behavior of the objective function around the set of optimal solutions and it translates to faster convergence rates. The way one should think about sharpness and similar parameters is data-dependent quantities that are usually either hard to compute or inaccessible. As these quantities are also (usually) unobservable and estimation is non-trivial yet impact the convergence rate, we would like our algorithms to be adaptive to these parameters without requiring them as input, i.e., the algorithm behaves automatically better when the data is better conditioned.
We show that the greedy algorithm for submodular maximization also provides better approximation guarantees as (our submodular analog to) sharpness of the objective function increases. While surprising at first, this is actually quite natural, once we understand the greedy algorithm as a discrete analog of ascent algorithms in continuous optimization, that is allowed to perform a fixed number of steps only: if the algorithm converges faster, than after a fixed number of steps ($k$ in the discrete case to be precise) its achieved approximation guarantee will be better. Then the key challenge is to identify a notion of sharpness that is meaningful in the context of submodular function maximization. We also show that the greedy algorithm automatically adapts to the submodular function’s sharpness.
The most basic notation of sharpness for submodular functions that we define is the following notion of monontone sharpness: There exists an optimal solution $S^\esx \subseteq V$ such that for all $S \subseteq V$ it holds:
\[\tag{monSharp} \sum_{e \in S^\esx \setminus S} \Delta_S(e) \geq \left( \frac{|S^\esx \setminus S|}{kc} \right)^{1/\theta} f(S^\esx),\]which then leads to a guarantee of the form:
\[f(S_g) \geq \left(1- \left(1-\frac{\theta}{c}\right)^{1/c}\right) f(S^\esx),\]which interpolates between the worst-case approximation factor $(1-1/\mathrm{e})$ and the best-case approximation factor $1$.
We also define tighter notions of sharpness that explain more of greedy’s performance, however their definitions are slightly more involved and beyond the scope of this summary. In the following figure we depict the performance of the greedy algorithm on three different tasks as well as how much of its performance is explained by various data-dependent measures - it can be seen that our most advanced notion of sharpness, called dynamic submodular sharpness, explains a significant portion of greedy’s performance.
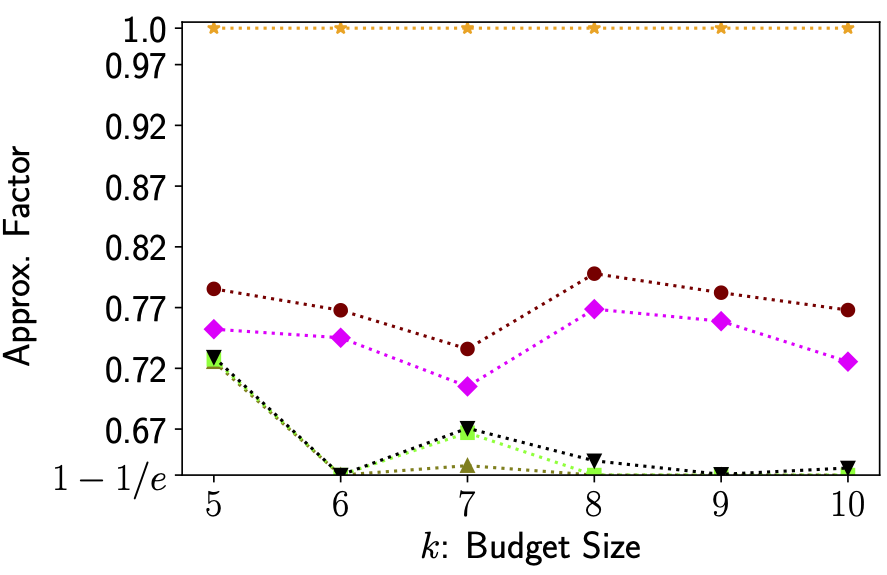
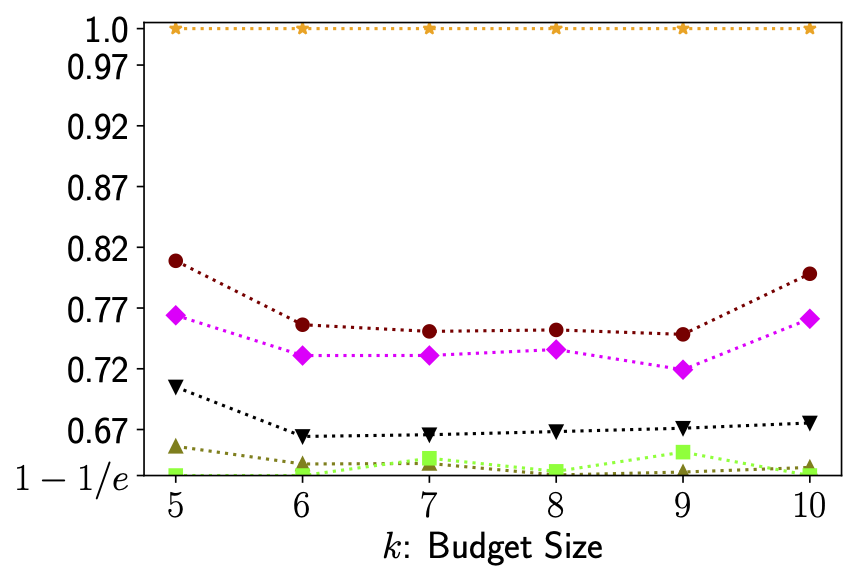

Figure 1. Image Clustering (left), Facility Location (middle), Parkison Telemonitoring (right). For each example we computed both the sharpness parameters and optimal solutions to compare predicted vs actual performance. In all three examples sharpness explains a significant portion of the greedy algorithm’s excess performance.
One final but important question that one might ask is: how many functions actually do satisfy sharpness? In convex optimization, by the Łojasiewicz Factorization Lemma (see [BDL] and references contained therein), basically almost all functions exhibit non-trivial sharpness; the same is true for the submodular case here, albeit in somewhat weaker form.
References
[NWF] Nemhauser, G. L., Wolsey, L. A., & Fisher, M. L. (1978). An analysis of approximations for maximizing submodular set functions—I. Mathematical programming, 14(1), 265-294. pdf
[NW] Nemhauser, G. L., & Wolsey, L. A. (1978). Best algorithms for approximating the maximum of a submodular set function. Mathematics of operations research, 3(3), 177-188. pdf
[CC] Conforti, M., & Cornuéjols, G. (1984). Submodular set functions, matroids and the greedy algorithm: tight worst-case bounds and some generalizations of the Rado-Edmonds theorem. Discrete applied mathematics, 7(3), 251-274. pdf
[CRV] Chatziafratis, V., Roughgarden, T., & Vondrák, J. (2017). Stability and recovery for independence systems. arXiv preprint arXiv:1705.00127. pdf
[BDL] Bolte, J., Daniilidis, A., & Lewis, A. (2007). The Łojasiewicz inequality for nonsmooth subanalytic functions with applications to subgradient dynamical systems. SIAM Journal on Optimization, 17(4), 1205-1223. pdf
Comments