Sharpness and Restarting Frank-Wolfe
TL;DR: This is an informal summary of our recent paper Restarting Frank-Wolfe with Alexandre D’Aspremont and Thomas Kerdreux, where we show how to achieve improved convergence rates under sharpness through restarting Frank-Wolfe algorithms.
Note: This summary is shorter than usual as I wrote a whole post about sharpness (aka Hölder Error Bounds) and conditional gradient methods that is strongly correlated with this paper some time back; for the sake non-duplication the interested reader is referred to Cheat Sheet: Hölder Error Bounds (HEB) for Conditional Gradients, which also explains the more technical aspects of our work in a significantly broader context.
What is the paper about and why you might care
We often want to solve constrained smooth convex optimization problems of the form
\[\min_{x \in P} f(x),\]where $P$ is some compact convex set and $f$ is a smooth function. If the considered function $f$ is strongly convex, then we can expect a linear rate of convergence of $O(\log 1/\varepsilon)$, i.e., it takes about $k \sim \log 1/\varepsilon$ iterations until $f(x_k) - f(x^\esx) \leq \varepsilon$ by using Away-Step Frank-Wolfe or Pairwise Conditional Gradients (see Cheat Sheet: Linear convergence for Conditional Gradients for more). However, in absence of strongly convexity we often have to fall back to the smooth and (non-strongly) convex case with a much lower rate of $O(1/\varepsilon)$ (without acceleration). In many cases this rate is considerably worse than what is empirically observed. To remedy this by providing a more fine-grained convergence analysis, in a recent paper [RA] analyzed convergence under sharpness (also known as the Hölder Error Bound (HEB) condition) which characterizes the behavior of $f$ around the optimal solutions:
Definition (Hölder Error Bound (HEB) condition). A convex function $f$ is satisfies the Hölder Error Bound (HEB) condition on $P$ with parameters $0 < c < \infty$ and $\theta \in [0,1]$ if for all $x \in P$ it holds: \[ c (f(x) - f^\esx)^\theta \geq \min_{y \in \Omega^\esx} \norm{x-y}. \]
It was shown that using the notion of sharpness, one can derive much better rates, covering the whole range between the sublinear rate of $O(1/\varepsilon)$ and the linear rate $O(\log 1/\varepsilon)$. Moreover, these rates can be realized with adaptive restart schemes, requiring no knowledge about the sharpness parameters.
To establish the link to strong convexity, note that strong convexity which is a global property implies sharpness (with appropriate parameterization) which has to hold only locally around the optimal solutions; the converse is not true. In fact, using sharpness one can show linear convergence for certain function classes of functions that are not strongly convex.
Our results
An open question was whether adaptive restarts can be also utilized to achieve a similar adaptive behavior for Conditional Gradient type methods that access the feasible region $P$ only through a linear programming oracle and this is precisely what we study in our recent work [KDP]. There we show that one can modify the Away-Step Frank Wolfe algorithm (and similarly Pairwise Conditional Gradients) by endowing them with scheduled restarts to automatically adapt to the function’s sharpness. For functions with optimal solutions contained in the strict relative interior of $P$ it even suffices to modify the (vanilla) Frank-Wolfe algorithm. By doing so we obtain, depending on the function’s sharpness parameters, convergence rates of the form $O(1/\varepsilon^p)$ or $O(\log 1/\varepsilon)$. In particular, similar to [RA], we can achieve linear convergence for functions that are sufficiently sharp but not strongly convex.
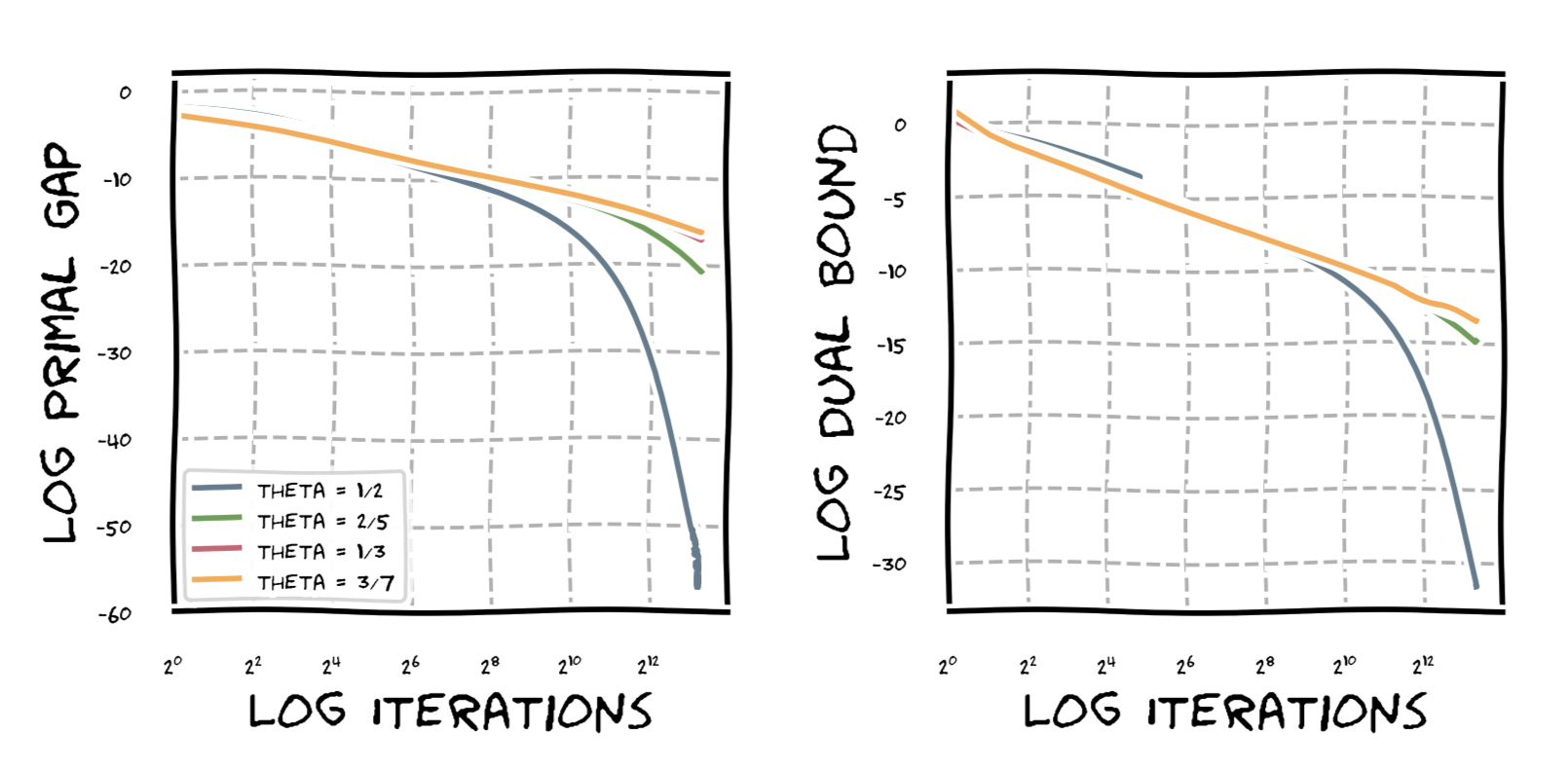
For illustration, the next graph shows the behavior of the Frank-Wolfe Algorithm under sharpness on the probability simplex of dimension $30$ and function $\norm{x}_2^{1/\theta}$. For $\theta = 1/2$, we observe linear convergence as expected, while for the other values of $\theta$ we observe various degrees of sublinear convergence of the form $O(1/\varepsilon^p)$ with $p \geq 1$.
References
[RA] Roulet, V., & d’Aspremont, A. (2017). Sharpness, restart and acceleration. In Advances in Neural Information Processing Systems (pp. 1119-1129). pdf
[KDP] Kerdreux, T., d’Aspremont, A., & Pokutta, S. (2018). Restarting Frank-Wolfe. to appear in Proceedings of AISTATS. pdf
Comments